2020年北京市中國人民大學附中高考數學模擬試卷（6月份）（三模）

一、選擇題共10小題，每小題4分，共40分.在每小題列出的四個選項中，選出符合題目要求的一項.

• 1．設集合P={3，log₂a}，Q={a,b}，若P∩Q={0}，則P∪Q=（　　）

  A．{3，0}

  B．{3，0，1}

  C．{3，0，2}

  D．{3，0，1，2}
  組卷：2059引用：104難度：0.9

  解析

• 2．若復數z=

  2

  1

  +

  3

  i

  ，則|z|=（　　）

  A． 1 2

  B． 3 2

  C．1

  D．2
  組卷：70引用：12難度：0.9

  解析

• 3．已知

  a

  =

  （

  1

  3

  ）

  2

  5

  ，

  b

  =

  （

  2

  5

  ）

  -

  1

  3

  ，

  c

  =

  lo

  g

  3

  2

  5

  ，則（　　）

  A．a＜b＜c

  B．c＜b＜a

  C．b＜c＜a

  D．c＜a＜b
  組卷：131引用：2難度：0.8

  解析

• 4．已知函數f（x）的圖象沿x軸向左平移2個單位后與函數y=2^x的圖象關于x軸對稱，若f（x₀）=-1，則x₀=（　　）

  A．-2

  B．2

  C．-log23

  D．log23
  組卷：124引用：2難度：0.8

  解析

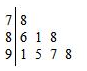• 5．為了解某年級400名女生五十米短跑情況，從該年級中隨機抽取8名女生進行五十跑測試，她們的測試成績（單位：秒）的莖葉圖（以整數部分為莖，小數部分為葉）如圖所示．由此可估計該年級女生五十米跑成績及格（及格成績為94秒）的人數為（　　）

  A．150

  B．250

  C．200

  D．50
  組卷：40引用：1難度：0.9

  解析

• 6．“

  φ

  =

  -

  π

  6

  ”是“函數

  f

  （

  x

  ）

  =

  sin

  （

  2

  x

  +

  π

  3

  ）

  （

  x

  ∈

  R

  ）

  與函數g（x）=cos（2x+φ）（x∈R）為同一函數”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：194引用：3難度：0.6

  解析

• 7．某四棱錐的三視圖如圖所示，則該四棱錐的體積是（　　）
  

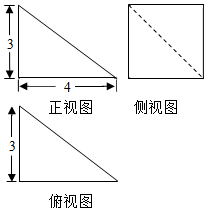
  A．12

  B．18

  C．24

  D．36
  組卷：55引用：3難度：0.5

  解析

三、解答題共6小題，共85分.解答應寫出文字說明、演算步驟或證明過程.

• 20．橢圓

  E

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率是

  5

  3

  ，過點P（0，1）作斜率為k的直線l,橢圓E與直線l交于A，B兩點，當直線l垂直于y軸時

  |

  AB

  |

  =

  3

  3

  ．
  （Ⅰ）求橢圓E的方程；
  （Ⅱ）當k變化時，在x軸上是否存在點M（m,0），使得△AMB是以AB為底的等腰三角形，若存在求出m的取值范圍，若不存在說明理由．
  組卷：173引用：8難度：0.5

  解析

• 21．在平面直角坐標系中，對于任意相鄰三點都不共線的有序整點列（整點即橫縱坐標都是整數的點）A（n）：A₁，A₂，A₃，…，A_n與B（n）：B₁，B₂，B₃，…，B_n，其中n≥3，若同時滿足：①兩點列的起點和終點分別相同；②線段A_iA_i+1⊥B_iB_i+1，其中i=1，2，3，…，n-1，則稱A（n）與B（n）互為正交點列．
  （Ⅰ）試判斷A（3）：A₁（0，2），A₂（3，0），A₃（5，2）與B（3）：B₁（0，2），B₂（2，5），B₃（5，2）是否互為正交點列，并說明理由；
  （Ⅱ）求證：A（4）：A₁（0，0），A₂（3，1），A₃（6，0），A₄（9，1）不存在正交點列B（4）；
  （Ⅲ）是否存在無正交點列B（5）的有序整數點列A（5）？并證明你的結論．
  組卷：108引用：2難度：0.1

  解析