當前位置：試卷中心 > 試卷詳情

2022-2023學年江蘇省徐州市高一（下）期中數學試卷

發布：2024/7/17 8:0:9

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知i為虛數單位，則i²⁰³³=（　　）
A．i B．-i C．1 D．-1
組卷：16引用：2難度：0.8
解析
2．△ABC的三個內角A，B，C所對邊的長分別為a,b,c,設向量
p
=
（
a
+
c
,
b
）
，
q
=
（
b
+
a
,
c
-
a
）
．若
p
∥
q
，則角C的大小為（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
π
2
組卷：252引用：6難度：0.8
解析
3．復數z滿足z（1+i）=|1-
3
i|，則復數z=（　　）
A．
2
（cos
π
4
+isin
π
4
） B．
2
（cos
3
π
4
+isin
3
π
4
）
C．
2
（cos
π
4
-isin
π
4
） D．
2
（cos
7
π
4
-isin
7
π
4
）
組卷：56引用：4難度：0.7
解析
4．定義：
|
a
×
b
|
=
|
a
|
|
b
|
sinθ
，其中θ為向量
a
，
b
的夾角，若
|
a
|
=
2
，
|
b
|
=
5
，
（
a
+
b
）
?
a
=
-
2
，則
|
a
×
b
|
=（　　）
A．6 B．-6 C．-8 D．8
組卷：28引用：2難度：0.8
解析
5．等腰三角形底和腰之比為黃金分割比的三角形稱為黃金三角形，它是最美的三角形．例如，正五角星由5個黃金三角形和一個正五邊形組成，且每個黃金三角形都是頂角為36°的等腰三角形，如圖所示，在黃金三角形ABC中，
BC
AC
=
5
-
1
2
．根據這些信息，可求得cos144°的值為（　　）
A．
1
-
5
4
B．
-
5
-
1
2
C．
-
5
+
1
4
D．
-
3
+
5
8
組卷：98引用：2難度：0.7
解析
6．已知cosα=
5
5
，sin（β-α）=
-
10
10
，α，β均為銳角，則β=（　　）
A．
π
4
B．
π
8
C．
π
3
D．
π
6
組卷：395引用：6難度：0.7
解析
7．已知點P是△ABC所在平面內一點，有下列四個等式：
甲：
PA
+
PB
+
PC
=
0
；乙：
PA
?
（
PA
-
PB
）
=
PC
?
（
PA
-
PB
）
；
丙：|
PA
|=|
PB
|=|
PC
|；丁：
PA
?
PB
=
PB
?
PC
=
PC
?
PA
．
如果只有一個等式不成立，則該等式為（　　）
A．甲 B．乙 C．丙 D．丁
組卷：604引用：11難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本大題共6小題，共70分.解答時應寫出必要的文字說明、證明過程或演算步驟.

21．已知函數為f（x）=asinx+bcosx,稱向量
p
=（a,b）為f（x）的特征向量，f（x）為
p
的特征函數．
（1）若
g
（
x
）
=
sin
（
x
+
π
3
）
+
cos
（
x
-
π
6
）
，求g（x）的特征向量；
（2）設向量
p
=
（
3
，-
1
）
，
q
=
（
1
，
3
）
的特征函數分別為p（x），q（x）．記函數h（x）=p（x）q（x）．
（i）求h（x）的單調增區間；
（ii）若方程
h
（
x
）
=
2
3
在（0，π）上的解為x₁，x₂，求cos（x₁-x₂）．
組卷：40引用：2難度：0.5
解析
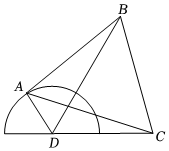22．為提升城市旅游景觀面貌，城建部門擬對一公園進行改造，已知原公園是直徑為200米的半圓，出入口在圓心D處，C點為一居民小區，CD距離為200米，按照設計要求，取圓弧上一點A，并以線段AC為一邊向圓外作等邊三角形ABC，使改造之后的公園成四邊形ABCD，并將△BCD區域建成免費開放的植物園，如圖所示．
（1）若DA⊥DC時，點B與出入口D的距離為多少米？
（2）A設計在什么位置時，免費開放的植物園區域△BCD面積最大？并求此最大面積．
組卷：106引用：3難度：0.4
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A． 2 （cos π 4 +isin π 4 ）	B． 2 （cos 3 π 4 +isin 3 π 4 ）
C． 2 （cos π 4 -isin π 4 ）	D． 2 （cos 7 π 4 -isin 7 π 4 ）

2022-2023學年江蘇省徐州市高一（下）期中數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知i為虛數單位，則i2033=（ ）

2．△ABC的三個內角A，B，C所對邊的長分別為a,b,c,設向量p=（a+c,b），q=（b+a,c-a）．若p∥q，則角C的大小為（ ）

3．復數z滿足z（1+i）=|1-3i|，則復數z=（ ）

4．定義：|a×b|=|a||b|sinθ，其中θ為向量a，b的夾角，若|a|=2，|b|=5，（a+b）?a=-2，則|a×b|=（ ）

6．已知cosα=55，sin（β-α）=-1010，α，β均為銳角，則β=（ ）

7．已知點P是△ABC所在平面內一點，有下列四個等式：甲：PA+PB+PC=0；乙：PA?（PA-PB）=PC?（PA-PB）；丙：|PA|=|PB|=|PC|；丁：PA?PB=PB?PC=PC?PA．如果只有一個等式不成立，則該等式為（ ）

四、解答題：本大題共6小題，共70分.解答時應寫出必要的文字說明、證明過程或演算步驟.

1．已知i為虛數單位，則i²⁰³³=（　　）

2．△ABC的三個內角A，B，C所對邊的長分別為a,b,c,設向量
p
=
（
a
+
c
,
b
）
，
q
=
（
b
+
a
,
c
-
a
）
．若
p
∥
q
，則角C的大小為（　　）

3．復數z滿足z（1+i）=|1-
3
i|，則復數z=（　　）

4．定義：
|
a
×
b
|
=
|
a
|
|
b
|
sinθ
，其中θ為向量
a
，
b
的夾角，若
|
a
|
=
2
，
|
b
|
=
5
，
（
a
+
b
）
?
a
=
-
2
，則
|
a
×
b
|
=（　　）

6．已知cosα=
5
5
，sin（β-α）=
-
10
10
，α，β均為銳角，則β=（　　）

7．已知點P是△ABC所在平面內一點，有下列四個等式：
甲：
PA
+
PB
+
PC
=
0
；乙：
PA
?
（
PA
-
PB
）
=
PC
?
（
PA
-
PB
）
；
丙：|
PA
|=|
PB
|=|
PC
|；丁：
PA
?
PB
=
PB
?
PC
=
PC
?
PA
．
如果只有一個等式不成立，則該等式為（　　）