2023-2024學(xué)年四川省瀘州市瀘縣一中高二（上）開學(xué)數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．已知向量

  a

  =

  （

  x

  ,

  1

  ）

  ，

  b

  =

  （

  2

  ，

  4

  ）

  ，若

  a

  ∥

  b

  ，則x=（　　）

  A． - 1 2

  B． 1 2

  C．-2

  D．2
  組卷：70引用：4難度：0.8

  解析

• 2．冪函數(shù)f（x）=（m²-3m-3）x^m在區(qū)間（0，+∞）上單調(diào)遞減，則下列說(shuō)法正確的是（　　）

  A．m=4	B．f（x）是減函數(shù)
  C．f（x）是奇函數(shù)	D．f（x）是偶函數(shù)
  組卷：639引用：5難度：0.7

  解析

• 3．設(shè)m,n是兩條不同的直線，α，β是兩個(gè)不同的平面，則下列結(jié)論中正確的是（　　）

  A．若m∥n,n∥α，則m∥α	B．若m∥α，n∥α，則m∥n
  C．若m∥n,m∥α，n∥β，則α∥β	D．若m⊥α，n⊥β，α⊥β，則m⊥n
  組卷：88引用：6難度：0.7

  解析

• 4．在△ABC中，D為BC上一點(diǎn)，且

  BD

  =

  1

  2

  DC

  ，則

  AD

  =（　　）

  A． AB + 1 3 AC

  B． AB - 1 3 AC

  C． 2 3 AB + 1 3 AC

  D． 1 3 AB + 2 3 AC
  組卷：135引用：3難度：0.9

  解析

• 5．已知

  sin

  （

  x

  -

  π

  4

  ）

  =

  5

  5

  ，則

  cos

  （

  2

  x

  -

  π

  3

  ）

  =（　　）

  A． 2 3 - 3 10

  B． 2 3 ± 3 10

  C． 3 3 + 4 10

  D． 3 3 ± 4 10
  組卷：131引用：2難度：0.6

  解析

• 6．已知向量

  a

  ，

  b

  滿足

  a

  ?

  b

  =

  0

  ，則

  a

  -

  b

  在

  a

  方向上的投影向量為（　　）

  A． - a

  B． 2 a

  C． 2 b

  D． a
  組卷：88引用：4難度：0.8

  解析

• 7．在直三棱柱ABC-A₁B₁C₁中，∠CAB=90°，AB=2

  2

  ，

  AC

  =

  1

  ，

  A

  A

  1

  =2，則直線AC₁與BA₁所成角的余弦值為（　　）

  A． 2 3 9

  B． 2 15 15

  C． 4 3 9

  D． 15 15
  組卷：20引用：3難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟．

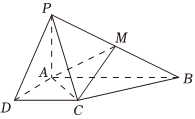• 21．已知四棱錐P-ABCD的底面為直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=1，AB=2，M是PB的中點(diǎn)．
  （1）證明：BC⊥平面PAC；
  （2）判斷直線CM與平面PAD的位置關(guān)系，并證明你的結(jié)論；
  （3）求二面角A-MC-B的余弦值．
  組卷：298引用：9難度：0.5

  解析

• 22．設(shè)平面向量

  a

  ，

  b

  的夾角為θ，

  a

  ?

  b

  =|

  a

  |?|

  b

  |sinθ．已知

  a

  =

  （

  sinx

  ,

  1

  ）

  ，

  b

  =

  （

  cosx

  ,

  1

  ）

  ，

  f

  （

  x

  ）

  =

  a

  ?

  b

  （

  0

  ≤

  x

  ＜

  3

  π

  4

  ）

  ．
  （1）求f（x）的解析式；
  （2）若f（x）g（x）=-cos2x,證明：不等式e^f（x）+f²（x）+f（x）＞2+2lng（x）在

  [

  π

  2

  ，

  3

  π

  4

  ）

  上恒成立．
  組卷：9引用：3難度：0.4

  解析