當(dāng)前位置：試卷中心 > 試卷詳情

2023年湖北省黃石市高考數(shù)學(xué)適應(yīng)性試卷

發(fā)布：2024/4/20 14:35:0

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．設(shè)集合M={x|log₂（x-1）＜0}，集合N={x|x≥-2}，則N∩M=（　　）
A．{x|-2≤x＜2} B．{x|x≥-2} C．{x|x＜2} D．{x|1＜x＜2}
組卷：121引用：13難度：0.9
解析
2．已知復(fù)數(shù)z₁=2-3i,z₁?z₂=-1-2i（i為虛數(shù)單位），則復(fù)數(shù)
z
2
等于（　　）
A．
4
13
+
7
13
i
B．
1
13
-
7
13
i
C．
4
5
+
7
5
i
D．
4
5
-
7
5
i
組卷：33引用：1難度：0.8
解析
3．已知向量
a
，
b
滿足
|
a
|
=
2
，
|
b
|
=
1
，
|
a
-
b
|
=
3
，則
＜
a
，
b
＞
=（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
組卷：353引用：5難度：0.7
解析
4．已知將函數(shù)
f
（
x
）
=
cos
（
ωx
+
φ
）
（
ω
＞
0
，
0
＜
φ
＜
π
2
）
向右平移
π
12
個單位長度后，所得圖象關(guān)于y軸對稱，且
f
（
0
）
=
2
2
，則當(dāng)ω取最小值時，函數(shù)f（x）的解析式為（　　）
A．
f
（
x
）
=
cos
（
5
x
+
π
4
）
B．
f
（
x
）
=
sin
（
9
x
-
π
4
）
C．
f
（
x
）
=
cos
（
3
x
+
π
4
）
D．
f
（
x
）
=
cos
（
1
3
x
+
π
4
）
組卷：256引用：5難度：0.6
解析
5．中國古代的武成王廟是專門祭祀姜太公以及歷代良臣名將的廟宇，這類廟宇的頂部構(gòu)造頗有講究，如圖是某武成王頂部的剖面直觀圖，其中A_iA′_i∥A_i+1A′_i+1，A_i+1B_i⊥A_iA′_i，A_iB_i=A_i+1B_i+1（i=1，2，3，4），數(shù)列
{
A
i
+
1
B
i
A
i
B
i
}
（i=1，2，3，4）是等差數(shù)列且
A
3
B
2
A
2
B
2
=
2
5
，若以A₁為坐標(biāo)原點，以
A
1
B
1
，
B
1
A
2
，分別為x,y軸正方向建立平面直角坐標(biāo)系，則直線A₁A₄的斜率是（　　）
A．0.4 B．0.45 C．0.5 D．0.55
組卷：154引用：3難度：0.5
解析

6．正方體ABCD-A₁B₁C₁D₁的棱長為2，正方形ABCD，A₁B₁C₁D₁的中心分別是O₁，O₂，且E，F(xiàn)，G，H分別是棱AD，BC，A₁B₁，C₁D₁上的動點（含端點），其中E，F(xiàn)關(guān)于點O₁對稱，G，H關(guān)于點O₂對稱，EF⊥GH，則下列結(jié)論錯誤的是（　　）

A．若四點E，F(xiàn)，G，H都在球O上，則球O表面積的最大值為12π

B．若四點E，F(xiàn)，G，H都在球O上，則球O體積的最小值為

C．四面體EFGH的所有棱長都相等

D．直線EG與HF所成角的余弦值的取值范圍是

[

，

]

組卷：44引用：2難度：0.5

解析

7．直線l與雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左，右兩支分別交于點A，B，與雙曲線的兩條漸近線分別交于點C，D（A，C，D，B從左到右依次排列），若OA⊥OB，且|AC|，|CD|，|DB|成等差數(shù)列，則雙曲線的離心率的取值范圍是（　　）
A．
[
10
2
，
+
∞
）
B．
[
2
2
，
10
]
C．
[
10
2
，
2
3
]
D．
[
10
，
+
∞
）
組卷：290引用：5難度：0.5
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

四、解答題：本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

21．已知橢圓C₁：
x
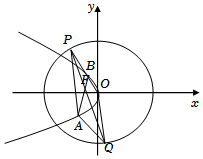2
a
2
+
y
2
b
2
=
1
（a＞b＞0）的離心率為
e
=
1
2
，且過點
P
（
-
1
，
3
2
）
．點P到拋物線C₂：y²=-2px（p＞0）的準(zhǔn)線的距離為
3
2
．
（1）求橢圓C₁和拋物線C₂的方程；
（2）如圖過拋物線C₂的焦點作F作斜率為k（k＞0）的直線交拋物線C₂于A，B兩點（點A在x軸下方），直線PF交橢圓C₁于另一點Q記△FBQ，△APQ的面積分別記為S₁、S₂．當(dāng)PF恰好平分∠APB時，求
S
1
S
2
的值．
組卷：443引用：5難度：0.2
解析
22．已知a＞2，函數(shù)
f
（
x
）
=
x
-
a
-
（
a
-
1
）
ln
x
a
，x＞0．
（1）求函數(shù)f（x）的單調(diào)區(qū)間和極值；
（2）設(shè)f（x）較小的零點為x₁，證明：
a
-
2
＜
x
1
＜
a
-
2
+
1
a
．
組卷：142引用：3難度：0.5
解析

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測評 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會員，資源免費下載

A． f （ x ） = cos （ 5 x + π 4 ）	B． f （ x ） = sin （ 9 x - π 4 ）
C． f （ x ） = cos （ 3 x + π 4 ）	D． f （ x ） = cos （ 1 3 x + π 4 ）

2023年湖北省黃石市高考數(shù)學(xué)適應(yīng)性試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．設(shè)集合M={x|log2（x-1）＜0}，集合N={x|x≥-2}，則N∩M=（ ）

2．已知復(fù)數(shù)z1=2-3i,z1?z2=-1-2i（i為虛數(shù)單位），則復(fù)數(shù)z2等于（ ）

3．已知向量a，b滿足|a|=2，|b|=1，|a-b|=3，則＜a，b＞=（ ）

4．已知將函數(shù)f（x）=cos（ωx+φ）（ω＞0，0＜φ＜π2）向右平移π12個單位長度后，所得圖象關(guān)于y軸對稱，且f（0）=22，則當(dāng)ω取最小值時，函數(shù)f（x）的解析式為（ ）

7．直線l與雙曲線x2a2-y2b2=1（a＞0，b＞0）的左，右兩支分別交于點A，B，與雙曲線的兩條漸近線分別交于點C，D（A，C，D，B從左到右依次排列），若OA⊥OB，且|AC|，|CD|，|DB|成等差數(shù)列，則雙曲線的離心率的取值范圍是（ ）

四、解答題：本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

22．已知a＞2，函數(shù)f（x）=x-a-（a-1）lnxa，x＞0．（1）求函數(shù)f（x）的單調(diào)區(qū)間和極值；（2）設(shè)f（x）較小的零點為x1，證明：a-2＜x1＜a-2+1a．

1．設(shè)集合M={x|log₂（x-1）＜0}，集合N={x|x≥-2}，則N∩M=（　　）

2．已知復(fù)數(shù)z₁=2-3i,z₁?z₂=-1-2i（i為虛數(shù)單位），則復(fù)數(shù)
z
2
等于（　　）

3．已知向量
a
，
b
滿足
|
a
|
=
2
，
|
b
|
=
1
，
|
a
-
b
|
=
3
，則
＜
a
，
b
＞
=（　　）

4．已知將函數(shù)
f
（
x
）
=
cos
（
ωx
+
φ
）
（
ω
＞
0
，
0
＜
φ
＜
π
2
）
向右平移
π
12
個單位長度后，所得圖象關(guān)于y軸對稱，且
f
（
0
）
=
2
2
，則當(dāng)ω取最小值時，函數(shù)f（x）的解析式為（　　）

22．已知a＞2，函數(shù)
f
（
x
）
=
x
-
a
-
（
a
-
1
）
ln
x
a
，x＞0．
（1）求函數(shù)f（x）的單調(diào)區(qū)間和極值；
（2）設(shè)f（x）較小的零點為x₁，證明：
a
-
2
＜
x
1
＜
a
-
2
+
1
a
．