2012年第12屆“子陵杯”七年級數學競賽試卷（二試）
發布：2024/4/20 14:35:0
一、仔細選一選（每小題3分，共36分）
-
1．在△ABC中，若∠A=∠B=40°，則∠C等于（ ）
組卷：70引用：8難度：0.9 -
2．計算a2a3正確的結果是（ ）
組卷：30引用：3難度：0.9 -
3．下列事件中，必然事件是（ ）
組卷：16引用：8難度：0.9 -
4．小明和哥哥并排站在鏡子前，小明看到鏡子中哥哥的球衣號碼如圖，那么哥哥球衣上的實際號碼是（ ）組卷：152引用：18難度：0.7 -
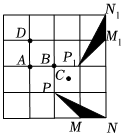5．在如圖4×4的正方形網格中，△MNP繞某點旋轉一定的角度，得到△M1N1P1，則其旋轉中心可能是（ ）組卷：3232引用：139難度：0.9 -
6．下列分解因式正確的是（ ）
組卷：875引用：57難度：0.9 -
7．若關于x,y的二元一次方程組
的解也是二元一次方程2x+3y=6的解，則k的值為（ ）x+y=5kx-y=9k組卷：16006引用：90難度：0.9 -
8．已知五條線段的長分別是1，2，3，4，5，若每次從中取出三條，分別以這三條線段為三邊，一共可以圍成不同三角形的個數是（ ）
組卷：44引用：2難度：0.9
三、認真答一答（共66分）
-
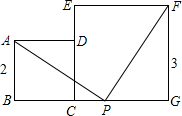25．如圖，正方形ABCD的邊CD在正方形ECGF的邊CE上，B、C、G三點在一條直線上，且邊長分別為2和3，在BG上截取GP=2，連接AP、PF．
（1）觀察猜想AP與PF之間的大小關系，并說明理由；
（2）圖中是否存在通過旋轉、平移、反射等變換能夠互相重合的兩個三角形？若存在，請說明變換過程；若不存在，請說明理由；
（3）若把這個圖形沿著PA、PF剪成三塊，請你把它們拼成一個大正方形，在原圖上畫出示意圖，并請求出這個大正方形的面積．組卷：294引用：27難度：0.1 -
26．閱讀與理解：
三角形的中線的性質：三角形的中線等分三角形的面積，
即如圖1，AD是△ABC中BC邊上的中線，
則．S△ABD=S△ACD=12S△ABC
理由：∵BD=CD，∴=S△ABD=12BD×AH=12CD×AH=S△ACD，12S△ABC
即：等底同高的三角形面積相等．
操作與探索
在如圖2至圖4中，△ABC的面積為a.
（1）如圖2，延長△ABC的邊BC到點D，使CD=BC，連接DA．若△ACD的面積為S1，則S1=（用含a的代數式表示）；
（2）如圖3，延長△ABC的邊BC到點D，延長邊CA到點E，使CD=BC，AE=CA，連接DE．若△DEC的面積為S2，則S2=（用含a的代數式表示），并寫出理由；
（3）在圖3的基礎上延長AB到點F，使BF=AB，連接FD，FE，得到△DEF（如圖4）．若陰影部分的面積為S3，則S3=（用含a的代數式表示）．
拓展與應用
如圖5，已知四邊形ABCD的面積是a,E、F、G、H分別是AB、BC、CD、DA的中點，求圖中陰影部分的面積？
組卷：1098引用：6難度：0.5