2022-2023學年廣東省惠州市惠州中學等四校聯考高二(上)月考數學試卷
發布:2024/12/22 18:30:3
一、選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.設全集為R,集合A={x|0<x<2},B={x|x≥1},則A∩(?RB)=( )
A.{x|0<x≤1} B.{x|0<x<1} C.{x|1≤x<2} D.{x|0<x<2} 組卷:7791引用:50難度:0.9 -
2.法國數學家棣莫弗(1667-1754)發現的公式(cosx+isinx)n=cosnx+isinnx推動了復數領域的研究.根據該公式,可得
=( )(cosπ8+isinπ8)4(1+i)A.-1+i B.1 C.-1-i D.-i 組卷:24引用:2難度:0.8 -
3.已知雙曲線E:
的一條漸近線方程為3x+2y=0,則雙曲線的焦距為( )x24-y2m=1A.4 B.6 C. 213D.13 組卷:78引用:4難度:0.8 -
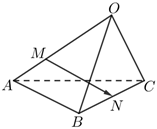 4.如圖所示,空間四邊形OABC中,,點M在OA上,且OA=a,OB=b,OC=c,N為BC中點,則OM=2MA等于( )MN
4.如圖所示,空間四邊形OABC中,,點M在OA上,且OA=a,OB=b,OC=c,N為BC中點,則OM=2MA等于( )MNA. 12a-23b+12cB. -23a+12b+12cC. 12a+12b-23cD. 23a+23b-12c組卷:240引用:25難度:0.7 -
5.已知兩點A(1,2),B(3,6),動點M在直線y=x上運動,則|MA|+|MB|的最小值為( )
A. 25B. 26C.4 D.5 組卷:634引用:12難度:0.7 -
6.在棱長為2的正方體ABCD-A1B1C1D1中,分別取棱AA1,A1D1的中點E,F,點G為EF上一個動點,則點G到平面ACD1的距離為( )
A. 32B. 3C.1 D. 33組卷:70引用:6難度:0.6 -
 7.如圖所示,該曲線W是由4個圓:(x-1)2+y2=1,(x+1)2+y2=1,x2+(y+1)2=1,x2+(y-1)2=1的一部分所構成,則下列敘述錯誤的是( )
7.如圖所示,該曲線W是由4個圓:(x-1)2+y2=1,(x+1)2+y2=1,x2+(y+1)2=1,x2+(y-1)2=1的一部分所構成,則下列敘述錯誤的是( )A.曲線W圍成的封閉圖形面積為4+2π B.若圓x2+y2=r2(r>0)與曲線W有4個交點,則 或2r=2C. 與?BD的公切線方程為?DEx+y-1-2=0D.曲線上的點到直線 的距離的最小值為3x+y+52+1=0組卷:131引用:5難度:0.5
四、解答題:本大題共6小題,共70分.解答應寫出文字說明,證明過程或演算步驟.
-
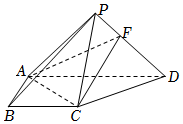 21.如圖,在四棱錐P-ABCD中,側面PAD⊥底面ABCD,側棱PA=PD=,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,2.PF=12FD
21.如圖,在四棱錐P-ABCD中,側面PAD⊥底面ABCD,側棱PA=PD=,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,2.PF=12FD
(1)求證:PB∥平面ACF;
(2)在線段PB上是否存在一點H,使得CH與平面ACF所成角的正弦值為?若存在,求出線段PH的長度;若不存在,請說明理由.66組卷:255引用:5難度:0.5 -
22.已知雙曲線C:
的右焦點為F(c,0),離心率為2,直線x2a2-y2b2=1(a>0,b>0)與雙曲線C的一條漸近線交于點P,且x=a2c.|PF|=3
(1)求雙曲線C的標準方程;
(2)設Q為雙曲線右支上的一個動點,證明:在x軸的負半軸上存在定點M,使得∠QFM=2∠QMF.組卷:76引用:4難度:0.3


