2023年山東省濟寧市泗水縣中考數學二模試卷

一、選擇題（下列各題的四個選項中，只有一項符合題意，請把正確選項前的字母填在答題紙上）

• 1．下列四個數中，最小的是（　　）

  A．-1

  B． - 2

  C．（-3）0

  D．-π
  組卷：16引用：1難度：0.7

  解析

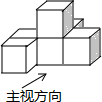• 2．由六個相同的立方體搭成的幾何體如圖所示，則它的主視圖是（　　）

  A．

  B．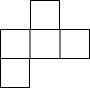

  C．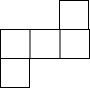

  D．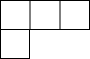
  組卷：308引用：5難度：0.9

  解析

• 3．下面是一位同學做的四道題：
  ①2a+3b=5ab；
  ②-（-2a²b³）⁴=-16a⁸b¹²；
  ③（a+b）³=a³+b³；
  ④（a-2b）²=a²-2ab+4b²
  其中做對的一道題的序號是（　　）

  A．①

  B．②

  C．③

  D．④
  組卷：91引用：4難度：0.9

  解析

• 4．某校規定學生的學期數學成績滿分為100分，其中研究性學習成績占40%，期末卷面成績占60%，小明的兩項成績（百分制）依次是90分，80分，則小明這學期的數學成績是（　　）

  A．80分

  B．87分

  C．84分

  D．88分
  組卷：50引用：2難度：0.8

  解析

• 5．已知α、β均為銳角，且滿足

  |

  sinα

  -

  1

  2

  |

  +

  （

  tanβ

  -

  1

  ）

  2

  =

  0

  ，則α+β=（　　）

  A．45°

  B．60°

  C．75°

  D．105°
  組卷：59引用：1難度：0.8

  解析

• 6．為響應“足球進校園”的號召，某校組織足球比賽，賽制為單循環形式（每兩個隊之間都要比賽一場），計劃安排28場比賽，則參賽的足球隊個數為（　　）

  A．6

  B．7

  C．8

  D．9
  組卷：447引用：4難度：0.7

  解析

• 7．如圖，Rt△ABC中，∠C=90°，利用尺規在BC，BA上分別截取BE，BD，使BE=BD；分別以D，E為圓心、以大于

  1

  2

  DE

  的長為半徑作弧，兩弧在∠CBA內交于點F；作射線BF交AC于點G．若CG=1，P為AB上一動點，則GP的最小值為（　　）

  A．2

  B． 1 2

  C．1

  D．無法確定
  組卷：316引用：15難度：0.5

  解析

三、解答題（解答題要求寫出必要的計算步驟或證明過程）

• 21．勾股定理是人類最偉大的十個科學發現之一，西方國家稱之為畢達哥拉斯定理．在我國古書《周髀算經》中就有“若勾三，股四，則弦五”的記載，我國漢代數學家趙爽為了證明勾股定理，創制了一幅“弦圖”（如圖1），后人稱之為“趙爽弦圖”，流傳至今．勾股定理內容為：如果直角三角形的兩條直角邊分別為a,b,斜邊為c,那么a²+b²=c²．
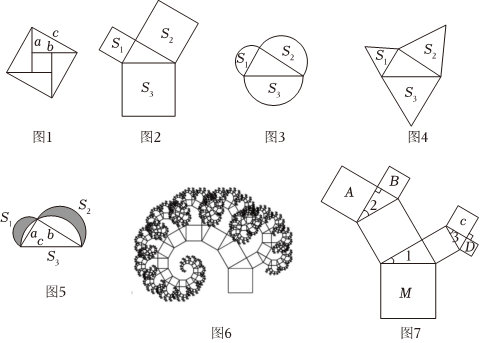  （1）如圖2、3、4，以直角三角形的三邊為邊或直徑，分別向外部作正方形、半圓、等邊三角形，這三個圖形中面積關系滿足S₁+S₂=S₃的有

  個；
  （2）如圖5所示，分別以直角三角形三邊為直徑作半圓，設圖中兩個月形圖案（圖中陰影部分）的面積分別為S₁，S₂，直角三角形面積為S₃，請判斷S₁，S₂，S₃的關系并證明；
  （3）如果以正方形一邊為斜邊向外作直角三角形，再以該直角三角形的兩直角邊分別向外作正方形，重復這一過程就可以得到如圖6所示的“勾股樹”．在如圖7所示的“勾股樹”的某部分圖形中，設大正方形M的邊長為定值m,四個小正方形A，B，C，D的邊長分別為a,b,c,d,已知∠1=∠2=∠3=∠α，則當∠α變化時，回答下列問題：（結果可用含m的式子表示）
  ①a²+b²+c²+d²=

  ；
  ②b與c的關系為

  ，a與d的關系為

  ．
  組卷：1084引用：3難度：0.3

  解析

• 22．如圖，拋物線y=ax²+bx+2與x軸交于A，B兩點，且OA=2OB，與y軸交于點C，連接BC，拋物線對稱軸為直線x=

  1

  2

  ，D為第一象限內拋物線上一動點，過點D作DE⊥OA于點E，與AC交于點F，設點D的橫坐標為m.
  （1）求拋物線的表達式；
  （2）當線段DF的長度最大時，求D點的坐標；
  （3）拋物線上是否存在點D，使得以點O，D，E為頂點的三角形與△BOC相似？若存在，求出m的值；若不存在，請說明理由．
  
  組卷：4851引用：18難度：0.4

  解析