2023年廣東省茂名市高州市高考數(shù)學(xué)一模試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合A={x|x+1＞0}，B={x|3x²+2x-1=0}，則A∩B=（　　）

  A．{1}

  B．{ 1 3 }

  C．{-1， 1 3 }

  D．{- 1 3 ，1}
  組卷：89引用：2難度：0.9

  解析

• 2．已知復(fù)數(shù)z=

  1

  3

  -

  4

  i

  ，則|

  z

  |=（　　）

  A． 1 5

  B． 1 9

  C． 1 16

  D． 1 25
  組卷：161引用：3難度：0.8

  解析

• 3．已知向量

  a

  =（-3，1），

  b

  =（m,m+2），若

  a

  ⊥

  b

  ，則|

  a

  +

  b

  |=（　　）

  A．2

  B．3

  C．4

  D．2 5
  組卷：447引用：4難度：0.7

  解析

• 4．已知M是拋物線C：x²=8y上一點(diǎn)，F(xiàn)為拋物線的焦點(diǎn)，點(diǎn)N（0，-4），若|MF|=|NF|，則△MFN的面積為（　　）

  A．8 2

  B．8 3

  C．12 2

  D．12 3
  組卷：106引用：3難度：0.7

  解析

• 5．已知tanα=

  2

  ，則

  sin

  3

  α

  sinα

  -

  si

  n

  2

  α

  =（　　）

  A．- 1 2

  B．- 1 3

  C． 1 3

  D． 1 2
  組卷：304引用：3難度：0.7

  解析

• 6．曲線f（x）=（a+2）x+

  1

  x

  （

  1

  2

  ＜x＜1）上存在點(diǎn)A，B，使得曲線f（x）在點(diǎn)A，B處的切線垂直，則a的取值范圍是（　　）

  A．（ 1 - 5 2 ， 1 + 5 2 ）	B．（-1，2）
  C．（-∞， - 5 - 1 2 ）	D．（ 5 - 1 2 ，2）
  組卷：179引用：1難度：0.5

  解析

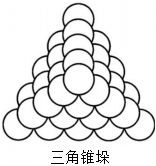• 7．朱世杰（1249年-1314年），字漢卿，號松庭，元代數(shù)學(xué)家、教育家，畢生從事數(shù)學(xué)教育，有“中世紀(jì)世界最偉大的數(shù)學(xué)家”之譽(yù)．他的一部名著《算學(xué)啟蒙》是中國最早的科普著作，該書中有名的是“堆垛問題”，其中有一道問題如下：今有三角錐垛果子，每面底子四十四個，問共積幾何？含義如下：把一樣大小的果子堆垛成正三棱錐形（如圖所示，給出了5層三角錐垛俯視示意圖），底面每邊44個果子，頂部僅一個果子，從頂層向下數(shù)，每
  層的果子數(shù)分別為1，3，6，10，15，21，…，共有44層，問全垛共有多少個果子？則該三角錐垛從頂層向下數(shù)前40層的果子總數(shù)為（　　）
  （參考公式：1+2²+3²+…+n²=

  1

  6

  n（n+1）（2n+1））

  A．12  341

  B．11  480

  C．10  280

  D．8  436
  組卷：66引用：3難度：0.6

  解析

四、解答題：本題共6小題，共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟。

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）經(jīng)過點(diǎn)M（-2，

  2

  ），其右焦點(diǎn)為F（c,0），下頂點(diǎn)為B，直線BF與橢圓C交于另一點(diǎn)D，且

  BF

  =

  3

  FD

  ．
  （1）求橢圓C的方程；
  （2）O為坐標(biāo)原點(diǎn)，過點(diǎn)M作x軸的垂線l₁，垂足為A，過點(diǎn)A的直線與C交于P，Q兩點(diǎn)，直線OP與l₁交于點(diǎn)H，直線OQ與l₁交于點(diǎn)G，設(shè)△APH的面積為S₁，△AQG的面積為S₂，試探究

  S

  1

  +

  S

  2

  S

  1

  S

  2

  是否存在最小值．若存在，求出此時直線PQ的方程；若不存在，請說明理由．
  組卷：126引用：3難度：0.3

  解析

• 22．已知函數(shù)f（x）=

  1

  2

  ax²-（1+2a）x+2（a+1）ln（x+1）+2a.
  （1）討論f（x）的單調(diào)性；
  （2）若a＜e-1，求證：f（x）＜

  1

  2

  ax²+2aln（x+1）-（1+4a）x+2e^x+1．
  組卷：148引用：2難度：0.3

  解析