2022-2023學年廣東省深圳市龍華中學高一(下)期中數學試卷
發布:2024/5/25 8:0:9
一、單選題(本大題共8小題,每小題5分,共40.0分。每小題只有一項是符合題目要求的)
-
1.已知向量
,a=(3,-1),則b=(1,-2)=( )-3a+2bA.(7,1) B.(-7,-1) C.(-7,1) D.(7,-1) 組卷:723引用:4難度:0.9 -
2.已知復數z=(m-3)+(m-1)i的模等于2,則實數m的值為( )
A.1或3 B.1 C.3 D.2 組卷:75引用:3難度:0.8 -
3.m,n是不同的直線,α,β是不重合的平面,下列說法正確的是( )
A.若α∥β,m?α,n?β,則m∥n B.若m,n?α,m∥β,n∥β,則α∥β C.m,n是異面直線,若m∥α,m∥β,n∥α,n∥β,則α∥β D.若α∥β,m∥α,則m∥β 組卷:115引用:3難度:0.9 -
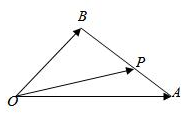 4.如圖,在△OAB中,P為線段AB上的一點,=xOP+yOA,且OB=3BP,則( )PA
4.如圖,在△OAB中,P為線段AB上的一點,=xOP+yOA,且OB=3BP,則( )PAA.x= ,y=2313B.x= ,y=1323C.x= ,y=1434D.x= ,y=3414組卷:825引用:13難度:0.9 -
5.已知圓錐的底面半徑為
,其側面展開圖為一個半圓,則該圓錐的母線長為( )2A.2 B.2 2C.4 D.4 2組卷:6946引用:44難度:0.8 -
6.已知向量
滿足a,b,若|a|=1,|b|=3,則向量|2a-b|=13與a的夾角為( )bA. 2π3B. π3C. 5π6D. π6組卷:152引用:2難度:0.7 -
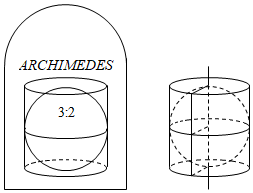 7.阿基米德(Archimedes,公元前287年-公元前212年)是古希臘偉大的數學家、物理學家和天文學家.他推導出的結論“圓柱內切球體的體積是圓柱體積的三分之二,并且球的表面積也是圓柱表面積的三分之二”是其畢生最滿意的數學發現,后人按照他生前的要求,在他的墓碑上刻著一個圓柱容器里放了一個球(如圖所示),該球與圓柱的兩個底面及側面均相切,圓柱的底面直徑與高都等于球的直徑,若球的體積為36π,則圓柱的體積為( )
7.阿基米德(Archimedes,公元前287年-公元前212年)是古希臘偉大的數學家、物理學家和天文學家.他推導出的結論“圓柱內切球體的體積是圓柱體積的三分之二,并且球的表面積也是圓柱表面積的三分之二”是其畢生最滿意的數學發現,后人按照他生前的要求,在他的墓碑上刻著一個圓柱容器里放了一個球(如圖所示),該球與圓柱的兩個底面及側面均相切,圓柱的底面直徑與高都等于球的直徑,若球的體積為36π,則圓柱的體積為( )A.36π B.45π C.54π D.63π 組卷:161引用:7難度:0.7
四、解答題(本大題共6小題,共70.0分。解答應寫出文字說明,證明過程或演算步驟)
-
 21.山頂有一座石塔BC,已知石塔的高度為a=20.2
21.山頂有一座石塔BC,已知石塔的高度為a=20.2
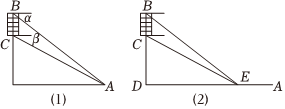
(1)如圖(1),若以B,C為觀測點,在塔頂B處測得地面上一點A的俯角為α=,在塔底C處測得A處的俯角為β=π4,求山的高度h.π6
(2)如圖(2),若將觀測點選在地面的直線AD上,其中D是塔頂B在地面上的正投影,當觀測點E在AD上滿足DE=120時,看BC的視角(即點B與點C仰角的差∠BEC)最大,求山的高度h.5組卷:36引用:1難度:0.6 -
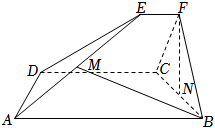 22.如圖,已知ABCD和CDEF都是直角梯形,AB∥DC,DC∥EF,AB=5,DC=3,EF=1,∠BAD=∠CDE=60°,二面角F-DC-B的平面角為60°.設M,N分別為AE,BC的中點.
22.如圖,已知ABCD和CDEF都是直角梯形,AB∥DC,DC∥EF,AB=5,DC=3,EF=1,∠BAD=∠CDE=60°,二面角F-DC-B的平面角為60°.設M,N分別為AE,BC的中點.
(1)求證:FN⊥平面ABCD;
(2)求直線BD與平面DCFE所成角的正弦值;
(3)求點D到平面ABFE的距離.組卷:157引用:3難度:0.6


