2020-2021學年廣東省深圳市寶安中學高一（下）期中數學試卷

一、解答題（共8小題，滿分40分）

• 1．向量

  |

  a

  |

  =

  3

  ，

  |

  b

  |

  =

  2

  3

  ，向量

  a

  與

  b

  的夾角是120°，則

  a

  ?

  b

  等于（　　）

  A．3

  B．-3

  C． - 3 3

  D． 3 3
  組卷：293引用：12難度：0.7

  解析

• 2．已知：空間四邊形ABCD如圖所示，E、F分別是AB、AD的中點，G、H分別是BC，CD上的點，且

  CG

  =

  1

  3

  BC

  ，

  CH

  =

  1

  3

  DC

  ，則直線FH與直線EG（　　）

  A．平行

  B．相交

  C．異面

  D．垂直
  組卷：605引用：8難度：0.9

  解析

• 3．設D為△ABC所在平面內一點，

  BC

  =

  2

  CD

  ，則（　　）

  A． AD = - 1 3 AB + 4 3 AC	B． AD = - 1 2 AB + 3 2 AC
  C． AD = 3 2 AB + 1 2 AC	D． AD = 3 2 AB - 1 2 AC
  組卷：1425引用：8難度：0.7

  解析

• 4．在△ABC中，a,b,c分別為內角A，B，C的對邊，若a=

  13

  ，c=3，且2absinC=

  3

  （

  b

  2

  +

  c

  2

  -

  a

  2

  ）

  ，則△ABC的面積為（　　）

  A．3 3

  B． 3 3 2

  C． 3

  D．6 3
  組卷：592引用：10難度：0.6

  解析

• 5．在△ABC中，角A，B，C所對的邊分別是a,b,c,已知a=2bcosC，則△ABC的形狀是（　　）

  A．等腰三角形	B．直角三角形
  C．等腰直角三角形	D．等腰或直角三角形
  組卷：399引用：15難度：0.9

  解析

• 6．下列命題中正確的個數有（　　）個
  （1）兩條直線a,b沒有公共點，那么a,b是異面直線；
  （2）若直線l上有無數個點不在平面α內，則l∥α；
  （3）空間中如果兩個角的兩邊分別對應平行，那么這兩個角相等或互補；
  （4）若直線l與平面α平行，則直線l與平面α內的任意一條直線都沒有公共點．

  A．0

  B．1

  C．2

  D．3
  組卷：83引用：2難度：0.7

  解析

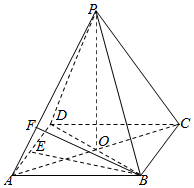• 7．如圖，已知四棱錐P-ABCD的底面是平行四邊形，AC交BD于點O，E為AD中點，F在PA上，AP=λAF，PC∥平面BEF，則λ的值為（　　）

  A．1

  B． 3 2

  C．2

  D．3
  組卷：486引用：8難度：0.7

  解析

四.解答題（合計70分，17題10分，其余每題12分）

• 21．在△ABC中，設角A，B，C的對邊長分別為a,b,c,已知

  sin

  A

  -

  sin

  B

  sin

  C

  =

  a

  -

  c

  a

  +

  b

  ．
  （1）求角B的值；
  （2）若△ABC為銳角三角形，且c=2，求△ABC的面積S的取值范圍．
  組卷：1040引用：18難度：0.6

  解析

• 22．已知函數g（x）=ax²-2ax+b（b＞0），在x∈[1，2]時最大值為1和最小值為0．設

  f

  （

  x

  ）

  =

  g

  （

  x

  ）

  x

  ．
  （1）求實數a,b的值；
  （2）若不等式g（2^x）-k?4^x+1≥0在x∈[-1，1]上恒成立，求實數k的取值范圍；
  （3）若關于x的方程

  f

  （

  |

  log

  2

  x

  |

  ）

  +

  2

  m

  |

  log

  2

  x

  |

  -

  3

  m

  -

  1

  =

  0

  有四個不同的實數解，求實數m的取值范圍．
  組卷：266引用：9難度：0.4

  解析