2018-2019學年湖南省長沙市天心區長郡教育集團九年級（上）第三次限時檢測數學試卷

一、選擇題（本大題共12小題，每小題3分，共36分在每小題所給出的四個選項中，恰有一項是符合題目要求的，請將正確選項前的字母代號填涂在答題卡相應位置上）

• 1．下列實數中，有理數是（　　）

  A． 3

  B．0.123

  C． 3 2

  D． π 2
  組卷：24引用：1難度：0.8

  解析

• 2．下列平面圖形中，既是軸對稱圖形，又是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：187引用：19難度：0.9

  解析

• 3．下列計算正確的是（　　）

  A． 3 - 8 =±2	B．（-3）0=1
  C．（-2a2b）2=-4a4b2	D．2a3÷（-2a）=-a3
  組卷：8引用：2難度：0.9

  解析

• 4．拋物線y=（x+2）²+3的頂點坐標是（　　）

  A．（-2，-3）

  B．（2，3）

  C．（-2，3）

  D．（2，-3）
  組卷：719引用：43難度：0.9

  解析

• 5．若△ABC∽△A?B?C?，∠A=40°，∠B=110°，則∠C?=（　　）

  A．40°

  B．110°

  C．70°

  D．30°
  組卷：217引用：15難度：0.9

  解析

• 6．若一個多邊形的內角和是900°，則這個多邊形的邊數是（　　）

  A．5

  B．6

  C．7

  D．8
  組卷：2178引用：110難度：0.9

  解析

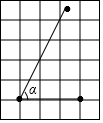• 7．在正方形網格中，∠α的位置如圖所示，則cosα的值是（　　）

  A． 5 5

  B． 2 5 5

  C． 1 2

  D． 2 2
  組卷：304引用：2難度：0.7

  解析

• 8．下列命題中，正確的是（　　）

  A．AB，CD是⊙O的弦，若AB=CD，則AB∥CD

  B．垂直于弦的直徑平分弦，并且平分弦所對的弧

  C．在同圓或等圓中，同弦或等弦所對的圓周角相等

  D．圓是軸對稱圖形，對稱軸是圓的每一條直徑
  組卷：53引用：1難度：0.6

  解析

三、解答題（本大題共8小題，第19、20題每題題6分；第21、22題每題8分；第23、24題每9分，第25、26題每題10分，共6分）

• 25．已知拋物線y=ax²+bx+4（a≠0）過點A（1，-1），B（5，-1），與y軸交于點C．
  （1）求拋物線的函數表達式．
  （2）如圖1，連接CB，以CB為邊作平行四邊形CBPQ，若點P在直線BC上方的拋物線上，Q為坐標平面內的一點，且平行四邊形CBPQ的面積為30，求點P的坐標；
  （3）如圖2，⊙O₁過A、B、C三點，AE為直徑，點M為⊙O₁上的一動點（不與點A，E重合），∠MBN為直角，邊BN與ME的延長線交于N，求線段BN長度的最大值．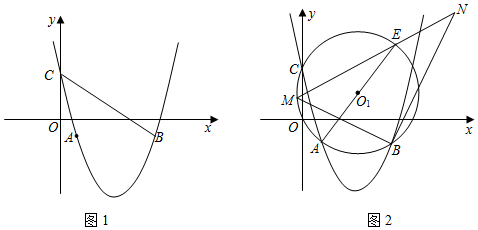
  
  組卷：366引用：2難度：0.4

  解析

• 26．定義：若存在實數對坐標（x,y）同時滿足一次函數y=px+q和反比例函數y=

  k

  x

  ，則二次函數y=px²+qx-k為一次函數和反比例函數的“聯姻”函數．
  （1）試判斷（需要寫出判斷過程）：一次函數y=-x+3和反比例函數y=

  2

  x

  是否存在“聯姻”函數，若存在，寫出它們的“聯姻”函數和實數對坐標．
  （2）已知：整數m,n,t滿足條件t＜n＜8m,并且一次函數y=（1+n）x+2m+2與反比例函數y=

  2015

  x

  存在“聯姻”函數y=（m+t）x²+（10m-t）x-2015，求m的值．
  （3）若同時存在兩組實數對坐標[x₁，y_1]和[x₂，y₂]使一次函數y=ax+2b和反比例函數y=

  -

  c

  x

  為“聯姻”函數，其中，實數a＞b＞c,a+b+c=0，設L=|x₁-x₂|，求L的取值范圍．
  組卷：938引用：2難度：0.1

  解析