2021-2022學年江西省南昌十中高一（下）期中數(shù)學試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．若集合A={x|x²-x-2＜0}，B={x|x²＜1}，則A∩B=（　　）

  A．A

  B．B

  C．（-1，0）

  D．（0，2）
  組卷：106引用：1難度：0.8

  解析

• 2．某校組織全體學生參加了主題為“奮斗百年路，啟航新征程”的知識競賽，隨機抽取了100名學生進行成績統(tǒng)計，發(fā)現(xiàn)抽取的學生的成績都在50分至100分之間，進行適當分組后（每組的取值區(qū)間均為左閉右開區(qū)間），畫出頻率分布直方圖（如圖），下列說法不正確的是（　　）
  

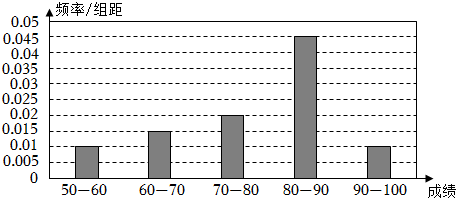
  A．在被抽取的學生中，成績在區(qū)間[90，100）內(nèi)的學生有10人

  B．這100名學生成績的眾數(shù)為85

  C．估計全校學生成績的平均分數(shù)為75

  D．這100名學生成績的中位數(shù)為 81 1 9
  組卷：39引用：2難度：0.7

  解析

• 3．sin15°cos135°+sin45°cos15°的值為（　　）

  A． - 3 2

  B． - 1 2

  C． 3 2

  D． 1 2
  組卷：129引用：2難度：0.8

  解析

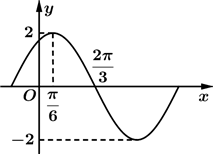• 4．已知函數(shù)f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜

  π

  2

  ）的圖象（部分）如圖所示，則f（x）的解析式是（　　）

  A．f（x）=2sin（x+ π 6 ）（x∈R）

  B．f（x）=2sin（2x+ π 6 ）（x∈R）

  C．f（x）=2sin（x+ π 3 ）（x∈R）

  D．f（x）=2sin（2x+ π 3 ）（x∈R）
  組卷：228引用：10難度：0.8

  解析

• 5．甲、乙去同一家藥店購買一種醫(yī)用外科口罩，已知這家藥店出售A，B，C三種醫(yī)用外科口罩，甲、乙購買A，B，C三種醫(yī)用口罩的概率分別如表：
  

  	購買A種醫(yī)用口罩	購買B種醫(yī)用口罩	購買C種醫(yī)用口罩
  甲	?	0.2	0.4
  乙	0.3	?	0.3

  則甲、乙購買的是同一種醫(yī)用外科口罩的概率為（　　）

  A．0.44

  B．0.40

  C．0.36

  D．0.32
  組卷：123引用：4難度：0.7

  解析

• 6．已知

  α

  ∈

  （

  -

  π

  2

  ，

  0

  ）

  ，

  sinα

  =

  -

  3

  5

  ，則

  tan

  α

  2

  =（　　）

  A．3

  B．-3

  C． 1 3

  D． - 1 3
  組卷：102引用：1難度：0.8

  解析

• 7．已知

  sin

  （

  α

  -

  π

  3

  ）

  =

  -

  2

  3

  ，則

  cos

  （

  2

  α

  +

  π

  3

  ）

  的值為（　　）

  A． 1 3

  B． 7 9

  C． - 1 9

  D． - 7 9
  組卷：195引用：2難度：0.8

  解析

四、解答題（本大題共6小題，共70分．解答時應(yīng)寫出文字說明、證明過程或演算步驟）

• 21．已知函數(shù)

  f

  （

  x

  ）

  =

  3

  sinωxcosωx

  +

  si

  n

  2

  ωx

  ，其中0＜ω＜6，且

  f

  （

  π

  12

  ）

  =

  1

  2

  ．
  （1）求函數(shù)f（x）的單調(diào)遞增區(qū)間；
  （2）若

  θ

  ∈

  （

  π

  12

  ，

  π

  6

  ）

  ，且

  f

  （

  θ

  ）

  =

  5

  6

  ，求

  cos

  （

  2

  θ

  +

  π

  12

  ）

  的值．
  組卷：272引用：2難度：0.5

  解析

• 22．已知函數(shù)f（x）=

  3

  sin（ωx+

  π

  6

  ）+2sin²（

  ωx

  2

  +

  π

  12

  ）-1（ω＞0）的相鄰兩對稱軸間的距離為

  π

  2

  ．
  （1）求f（x）的解析式；
  （2）將函數(shù)f（x）的圖像向右平移

  π

  6

  個單位長度，再把各點的橫坐標縮小為原來的

  1

  2

  （縱坐標不變），得到函數(shù)y=g（x）的圖像，當x∈[-

  π

  12

  ，

  π

  6

  ]時，求函數(shù)g（x）的值域；
  （3）對于第（2）問中的函數(shù)g（x），記方程g（x）=

  4

  3

  在x∈[

  π

  6

  ，

  4

  π

  3

  ]上的根從小到大依次為x₁，x₂，…，x_n，若m=x₁+2x₂+2x₃+…+2x_n-1+x_n，試求n與m的值．
  組卷：426引用：9難度：0.5

  解析