2022-2023學年北京市順義一中高二（下）月考數學試卷（3月份）

一、選擇題（共10小題，每小題5分，滿分50分）

• 1．在數列{a_n}中，a_n+1=a_n+2，且a₁=1，則a₄等于（　　）

  A．8

  B．6

  C．9

  D．7
  組卷：405引用：9難度：0.9

  解析

• 2．函數f（x）=

  x

  在x=1處的導數f′（1）等于（　　）

  A．- 1 2

  B． 1 2

  C．1

  D．2
  組卷：160引用：5難度：0.8

  解析

• 3．設等差數列{a_n}滿足a₃=5，a₁₀=-9，S_n是數列{a_n}的前n項和，則使得S_n最大的序號n=（　　）

  A．4

  B．5

  C．6

  D．7
  組卷：437引用：9難度：0.9

  解析

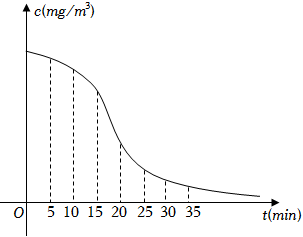• 4．降低室內微生物密度的有效方法是定時給室內注入新鮮空氣，即開窗通風換氣．在某室內，空氣中微生物密度（c）隨開窗通風換氣時間（t）的關系如圖所示，則下列時間段內，空氣中微生物密度變化的平均速度最快的是（　　）

  A．[5，10]

  B．[5，15]

  C．[5，20]

  D．[5，35]
  組卷：253引用：5難度：0.7

  解析

• 5．四位同學返校看望老師，由于時間關系，只見到語文，數學，英語三位老師，于是他們邀請老師一起照相，三位老師坐中間共有多少種排列方式（　　）

  A．90

  B．120

  C．144

  D．216
  組卷：109引用：3難度：0.9

  解析

• 6．已知x=1是函數f（x）=x³-3ax+2的極小值點，那么函數f（x）的極大值為（　　）

  A．0

  B．1

  C．2

  D．4
  組卷：308引用：6難度：0.6

  解析

• 7．設數列{a_n}的前n項和為S_n，則“對任意n∈N*，a_n＞0”是“數列{S_n}為遞增數列”的（　　）

  A．充分不必要條件

  B．必要不充分條件

  C．充分必要條件

  D．既不是充分也不是必要條件
  組卷：1136引用：6難度：0.7

  解析

三、解答題（共6小題，滿分75分）

• 20．設函數f（x）=lnx+1，g（x）=ax+2，a∈R，記F（x）=f（x）-g（x）．
  （1）求曲線y=f（x）在x=1處的切線方程；
  （2）求函數F（x）的單調區間；
  （3）若函數f（x）=lnx+1的圖象恒在g（x）=ax+2的圖象的下方，求實數a的取值范圍．
  組卷：193引用：5難度：0.6

  解析

• 21．已知有窮數列A：a₁，a₂，…，a_N（N∈N^*，N≥3）滿足a_i∈{-1，0，1}（i=1，2，…，N）．給定正整數m,若存在正整數s,t（s≠t），使得對任意的k∈{0，1，2，…，m-1}，都有a_s+k=a_t+k，則稱數列A是m-連續等項數列．
  （1）判斷數列A：-1，1，0，1，0，1，-1是否為3-連續等項數列？是否為4-連續等項數列？說明理由；
  （Ⅱ）若項數為N的任意數列A都是2-連續等項數列，求N的最小值；
  （Ⅲ）若數列A：a₁，a₂，…，a_N不是4-連續等項數列，而數列A₁：a₁a₂，…，a_N，-1，數列A₂：a₁a₂，…，a_N，0與數列A₃：a₁，a₂，…，a_N，1都是4-連續等項數列，且a₃=0，求a_N的值．
  組卷：372引用：7難度：0.2

  解析