2022-2023學年浙江省北斗聯盟高二（下）期中數學試卷

一、單選題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合

  A

  =

  {

  -

  2

  ，-

  1

  ，

  0

  ，

  1

  ，

  2

  }

  ，

  B

  =

  {

  x

  |

  -

  3

  ≤

  x

  ≤

  1

  }

  ，則A∩B=（　　）

  A．{-2，-1，0，1}	B．{-1，0，1}
  C．{0，1}	D．{-2，-1，0，1，2}
  組卷：82引用：3難度：0.8

  解析

• 2．設復數z滿足z?（1+2i）=5，則z的虛部是（　　）

  A．2

  B．2i

  C．-2

  D．-2i
  組卷：186引用：10難度：0.8

  解析

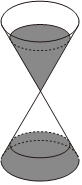• 3．沙漏是我國古代的一種計時工具，是用兩個完全相同的圓錐頂對頂疊放在一起組成的（如右圖）．在一個圓錐中裝滿沙子，放在上方，沙子就從頂點處漏到另一個圓錐中，假定沙子漏下來的速度是恒定的．已知一個沙漏中沙子全部從一個圓錐中漏到另一個圓錐中需總時長為1小時，當上方圓錐中沙子漏至圓錐高度的一半時，所需時間為（　　）

  A． 1 3 小時

  B． 7 8 小時

  C． 26 27 小時

  D． 8 9 小時
  組卷：145引用：8難度：0.6

  解析

• 4．平面向量

  a

  與

  b

  相互垂直，已知

  a

  =（6，-8），

  |

  b

  |

  =

  5

  ，且

  b

  與向量（1，0）的夾角是鈍角，則

  b

  =（　　）

  A．（-3，-4）

  B．（4，3）

  C．（-4，3）

  D．（-4，-3）
  組卷：519引用：12難度：0.7

  解析

• 5．定義運算：

  a 1	a 2
  a 3	a 4

  =a₁a₄-a₂a₃，將函數f（x）=

  3	cos x 2
  1	sin x 2

  的圖象向左平移m（m＞0）的單位后，所得圖象關于y軸對稱，則m的最小值是（　　）

  A． π 3

  B． 2 π 3

  C． 4 π 3

  D． 7 π 3
  組卷：82引用：6難度：0.9

  解析

• 6．概率論起源于博弈游戲.17世紀，曾有一個“賭金分配“的問題：博弈水平相當的甲、乙兩人進行博弈游戲每局比賽都能分出勝負，沒有平局．雙方約定，各出賭金48枚金幣，先贏3局者可獲得全部賭金；但比賽中途因故終止了，此時甲贏了2局，乙贏了1局．向這96枚金幣的賭金該如何分配？數學家費馬和帕斯卡都用了現在稱之為“概率“的知識，合理地給出了賭金分配方案．該分配方案是（　　）

  A．甲48枚，乙48枚	B．甲64枚，乙32枚
  C．甲72枚，乙24枚	D．甲80枚，乙16枚
  組卷：331引用：6難度：0.8

  解析

• 7．若a=log₂3，b=log₃4，c=log₄5，則a、b、c的大小關系是（　　）

  A．a＜b＜c

  B．b＜c＜a

  C．b＜a＜c

  D．c＜b＜a
  組卷：373引用：3難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  過點

  M

  （

  3

  ，

  2

  ）

  ，且右焦點為F（2，0）．
  （1）求雙曲線C的方程：
  （2）過點F的直線l與雙曲線C的右支交于A，B兩點，交y軸于點P，若

  PA

  =

  m

  AF

  ，

  PB

  =

  n

  BF

  ，求證：m+n為定值．
  （3）在（2）的條件下，若點Q是點P關于原點O的對稱點，求三角形QAB的面積的取值范圍．
  組卷：67引用：1難度：0.5

  解析

• 22．已知函數f（x）=alnx+

  1

  x

  ，a∈R．
  （1）當a=1時，求函數f（x）的單調區間；
  （2）若f（x）有經過原點的切線，求a的取值范圍及切線的條數，并說明理由．
  （3）設函數g（x）=f（x）-x的兩個極值點分別為x₁，x₂，且滿足

  g

  （

  x

  1

  ）

  -

  g

  （

  x

  2

  ）

  x

  1

  -

  x

  2

  ≤

  2

  e

  e

  2

  -

  1

  a-2，求實數a的取值范圍．
  組卷：256引用：2難度：0.3

  解析