2022-2023學年山西省忻州市定襄縣八年級(上)期末數學試卷
發布:2024/12/10 16:30:7
一.選擇題(本大題共10個小題,每小題3分,共30分。在每個小題給出的四個選項中,只有一項符合題目要求,請選出并在答題卡上將該選項涂黑)
-
1.若一個三角形的兩邊長分別為7和9,則此三角形第三邊的長可能為( )
A.1 B.7 C.16 D.17 組卷:166引用:6難度:0.6 -
2.圍棋起源于中國,古代稱之為“弈”,至今已有四千多年的歷史,下列由黑白棋子擺成的圖案是軸對稱圖形的是( )
A. 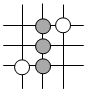
B. 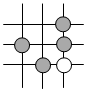
C. 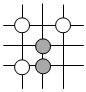
D. 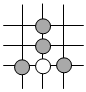 組卷:3703引用:89難度:0.9
組卷:3703引用:89難度:0.9 -
3.下列運算結果正確的是( )
A.x3?x4=x12 B.(-2x2)3=-8x6 C.x6÷x3=x2 D.x2+x3=x5 組卷:1031引用:12難度:0.8 -
 4.2022年11月18日,“芯科技,創未來”2022中國汽車芯片高峰論壇在中國電科智能科技園舉行.中國電科協同相關企業,發布了FPGA,DSP,MCU等數十款汽車電子產品,發布的車規級高安全FPGA芯片,采用28nm(1nm=10-9m)國產工藝,可應用于汽車疲勞駕駛預警、車載信息娛樂等領域.將數據“28nm”轉換成米用科學記數法表示為( )
4.2022年11月18日,“芯科技,創未來”2022中國汽車芯片高峰論壇在中國電科智能科技園舉行.中國電科協同相關企業,發布了FPGA,DSP,MCU等數十款汽車電子產品,發布的車規級高安全FPGA芯片,采用28nm(1nm=10-9m)國產工藝,可應用于汽車疲勞駕駛預警、車載信息娛樂等領域.將數據“28nm”轉換成米用科學記數法表示為( )A.2.8×10-10m B.28×10-9m C.2.8×10-8m D.2.8×10-7m 組卷:175引用:4難度:0.9 -
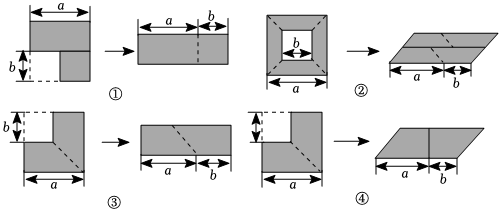 5.如圖,陰影部分是在一個邊長為a的大正方形中剪去一個邊長為b的小正方形后得到的圖形,將陰影部分通過割、拼,形成新的圖形.給出下列四種割拼方法,每種割拼方法都能夠驗證平方差公式,其中用到的數學思想是( )
5.如圖,陰影部分是在一個邊長為a的大正方形中剪去一個邊長為b的小正方形后得到的圖形,將陰影部分通過割、拼,形成新的圖形.給出下列四種割拼方法,每種割拼方法都能夠驗證平方差公式,其中用到的數學思想是( )A.數形結合思想 B.分類思想 C.公理化思想 D.函數思想 組卷:320引用:4難度:0.7 -
6.將關于x的分式方程
=3x-2-1去分母、去括號后所得整式方程正確的是( )52-xA.3=-5-x+2 B.3=-5-x-2 C.3=5-x+2 D.3=5-x-2 組卷:269引用:3難度:0.7 -
7.永祚寺雙塔,又名凌霄雙塔,是我市現存最高的古建筑,均為十三層八角形樓閣式磚塔,如圖的正八邊形是雙塔平面示意圖,其每個內角的度數為( )

A.80° B.100° C.120° D.135° 組卷:180引用:3難度:0.8 -
8.把分式
中的a,b都擴大到原來的5倍,則分式的值( )aba+bA.不變 B.擴大到原來的25倍 C.縮小到原來的 15D.擴大到原來的5倍 組卷:276引用:4難度:0.7
三、解答題(本大題共8個小題,共75分.解答應寫出文字說明、證明過程或演算步驟)
-
23.綜合與實踐
在等腰三角形紙片ABC中,AB=AC,∠BAC=36°.現要將其剪成三張小紙片,使每張小紙片都是等腰三角形(不能有剩余).下面是小文借助尺規解決這一問題的過程,請閱讀后完成相應的任務.作法:如圖1.
①分別作AB,AC的垂直平分線,交于點P;
②連接PA,PB,PC.
結論:沿線段PA,PB,PC剪開,即可得到三個等腰三角形.
理由:∵點P在線段AB的垂直平分線上,
∴.(依據)
同理,得PA=PC.
∴PA=PB=PC.
∴△PAB,△PBC,△PAC都是等腰三角形.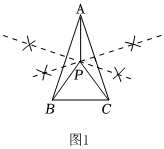
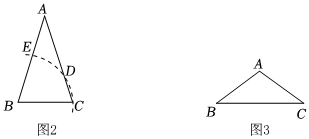
任務:
(1)上述過程中,橫線上的結論為 ,括號中的依據為 .
(2)受小文的啟發,同學們想到另一種思路:如圖2,以點B為圓心,BC長為半徑作弧,交AC于點D,交AB于點E.在此基礎上構造兩條線段(以圖中標有字母的點為端點)作為裁剪線,也可解決問題.請在圖2中畫出一種裁剪方案,并求出得到的三個等腰三角形及相應頂角的度數.
(3)如圖3,在等腰三角形紙片ABC中,AB=AC,∠BAC=108°,請在圖3中設計出一種裁剪方案,將該三角形紙片分成三個等腰三角形.(要求:尺規作圖,保留作圖痕跡,不寫作法,說明裁剪線)組卷:126引用:2難度:0.2 -
24.在直線m上依次取互不重合的三個點D,A,E,在直線m上方有AB=AC,且滿足∠BDA=∠AEC=∠BAC=α.
(1)如圖1,當α=90°時,猜想線段DE,BD,CE之間的數量關系是 ;
(2)如圖2,當0<α<180時,問題(1)中結論是否仍然成立?如成立,請你給出證明;若不成立,請說明理由;
(3)拓展與應用:如圖3,當α=120°時,點F為∠BAC平分線上的一點,且AB=AF,分別連接FB,FD,FE,FC,試判斷△DEF的形狀,并說明理由.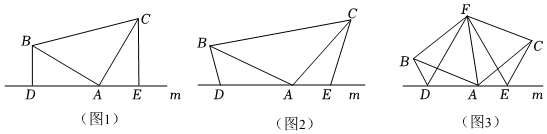 組卷:6719引用:15難度:0.3
組卷:6719引用:15難度:0.3


