2022-2023學年黑龍江省大慶市龍鳳區八年級（下）期中數學試卷

一、單選題（每小題3分，共30分

• 1．下列關于x的方程是一元二次方程的是（　　）

  A．x-1=3（x-2）

  B． 1 x +x2=0

  C．a2x+c=0

  D．x2-2x=0
  組卷：39引用：3難度：0.8

  解析

• 2．射擊運動員射擊一次，命中靶心，這個事件是（　　）

  A．必然事件

  B．不可能事件

  C．隨機事件

  D．確定性事件
  組卷：105引用：12難度：0.7

  解析

• 3．若關于x的方程x²-kx+3=0有一個根為-1，則k的值為（　　）

  A．-4

  B．-2

  C．2

  D．4
  組卷：154引用：2難度：0.7

  解析

• 4．已知一菱形周長為40cm,它的兩對角線長之比為3：4，則該菱形面積為（　　）

  A．38cm2

  B．40cm2

  C．48cm2

  D．96cm2
  組卷：214引用：6難度：0.6

  解析

• 5．一元二次方程x²-6x+1=0，配方后可變形為（　　）

  A．（x-3）2=7

  B．（x-6）2=8

  C．（x-3）2=10

  D．（x-3）2=8
  組卷：132引用：4難度：0.7

  解析

• 6．下列四個命題中，假命題的是（　　）

  A．有三個角是直角的四邊形是矩形

  B．對角線互相垂直平分且相等的四邊形是正方形

  C．四條邊都相等的四邊形是菱形

  D．順次連接等腰梯形各邊中點，得到一個矩形
  組卷：39引用：6難度：0.9

  解析

• 7．等腰三角形的底和腰是方程x²-7x+10=0的兩根，則這個三角形的周長為（　　）

  A．9

  B．12

  C．9或12

  D．不能確定
  組卷：72引用：2難度：0.7

  解析

• 8．根據下列表格的對應值：
  

  x	1	1.1	1.2	1.3
  x2+12x-15	-2	-0.59	0.84	2.29

  由此可判斷方程x²+12x-15=0必有一個根滿足（　　）

  A．1＜x＜1.1

  B．1.1＜x＜1.2

  C．1.2＜x＜1.3

  D．x＞1.3
  組卷：2525引用：34難度：0.5

  解析

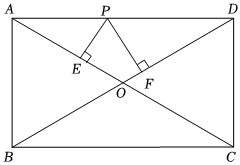• 9．已知：如圖，矩形ABCD中，AB=5，BC=12，對角線AC、BD相交于點O，點P是線段AD上任意一點，且PE⊥AC于點E，PF⊥BD于點F，則PE+PF等于（　　）

  A．6

  B．5

  C． 60 13

  D． 60 12
  組卷：1063引用：5難度：0.5

  解析

三、解答題（共66分）

• 27．如圖，四邊形ABCD、AEFM都是正方形，連接BE、DM．
  （1）判斷線段DM、BE的關系并證明．
  （2）連接DE、EM、MB、BD，順次連接各邊中點G、H、Q、N，試判斷四邊形GHQN的形狀，并說明理由．
  組卷：276引用：4難度：0.6

  解析

• 28．閱讀下列材料：利用完全平方公式，將多項式x²+bx+c變形為（x+m）²+n的形式，然后由（x+m）²≥0就可求出多項式x²+bx+c的最小值．
  例題：求x²-12x+37的最小值．
  解：x²-12x+37=x²-2?6+6²-6²+37=（x-6）²+1．
  因為不論x取何值，（x-6）²總是非負數，即（x-6）²≥0．
  所以（x-6）²+1≥1．
  所以當x=6時，x²-12x+37有最小值，最小值是1．
  根據上述材料，解答下列問題：
  （1）填空：x²-6x+

  =（x-

  ）²．
  （2）將x²+10x-2變形為（x+m）²+n的形式，并求出x²+10x-2的最小值．
  （3）如圖所示的第一個長方形邊長分別是2a+5、3a+2，面積為S₁；如圖所示的第二個長方形邊長分別是5a、a+5，面積為S₂．試比較S₁與S₂的大小，并說明理由．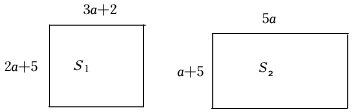
  
  組卷：118引用：3難度：0.6

  解析