2021-2022學年上海市虹口高級中學高一（下）期末數學試卷

一、填空題：（4*10=40分）

• 1．設復數z滿足i?z=3+2i,其中i為虛數單位，則Imz=

  ．
  組卷：43引用：2難度：0.9

  解析

• 2．已知向量

  a

  =（-1，1），

  b

  =（m,2），若存在實數λ，使得

  a

  =

  λ

  b

  ，則實數m的值為

  ．
  組卷：150引用：2難度：0.7

  解析

• 3．已知

  |

  b

  |

  =

  2

  ，

  a

  ?

  b

  =

  -

  4

  ，則向量

  a

  在向量

  b

  方向上的數量投影為

  ．
  組卷：61引用：2難度：0.8

  解析

• 4．將邊長為2的正方形ABCD水平放置，得到的直觀圖A'B'C'D'的面積為

  ．
  組卷：24引用：2難度：0.8

  解析

• 5．已知復數

  z

  1

  =

  -

  3

  +

  i

  ，若復數z滿足2iz=z₁，則復數z的輻角主值為

  ．
  組卷：189引用：1難度：0.8

  解析

• 6．已知復數z滿足：i+

  2

  +

  i

  z

  =0（i為虛數單位），則|z|=

  ．
  組卷：321引用：3難度：0.8

  解析

三、解答題（6+8+8+8+10=40分）

• 19．已知向量

  a

  =

  （

  cos

  2

  θ

  ，-

  2

  ）

  ，

  b

  =

  （

  1

  ，-

  sin

  2

  θ

  ）

  ，

  m

  =

  a

  ?

  b

  +

  2

  ，在復平面坐標系中，i為虛數單位．復數z₁=

  m

  +

  i

  1

  -

  i

  對應的點為Z₁．
  （1）求|z₁|；
  （2）若點Z為曲線

  |

  z

  -

  2

  z

  1

  |=1（

  z

  1

  為z₁的共軛復數）上的動點，求Z與Z₁之間距離的取值范圍．
  組卷：40引用：1難度：0.7

  解析

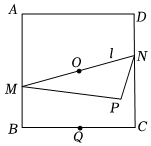• 20．如圖，已知正方形ABCD邊長為2，過中心O的直線l與兩邊AB、CD分別交于點M、N．
  （1）求

  BD

  ?

  DC

  的值；
  （2）若Q是BC的中點，求

  QM

  ?

  QN

  的取值范圍；
  （3）若P是平面上一點，且滿足2

  OP

  =λ

  OB

  +（1-λ）

  OC

  ，求

  PM

  ?

  PN

  的最小值．
  組卷：178引用：8難度：0.5

  解析