2019-2020學(xué)年新疆烏魯木齊九中九年級(jí)（上）第二次月考數(shù)學(xué)試卷
發(fā)布：2024/8/11 11:0:4
一、單選題（每小題5分，共45分）
-
1．觀察下列圖形，既是軸對(duì)稱圖形又是中心對(duì)稱圖形的有（ ）
組卷：301引用：72難度：0.9 -
2．二次函數(shù)y=-3（x+1）2-2的頂點(diǎn)坐標(biāo)是（ ）
組卷：1856引用：21難度：0.9 -
3．把拋物線y=5x2向左平移2個(gè)單位，再向上平移3個(gè)單位，得到的拋物線是（ ）
組卷：2603引用：47難度：0.8 -
4．若二次函數(shù)y=x2-6x+c的圖象過(guò)A（-1，y1），B（3，y2），C（3+
，y3），則y1，y2，y3的大小關(guān)系是（ ）2組卷：572引用：8難度：0.9 -
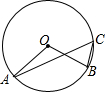5．如圖，OA，OB是⊙O的半徑，點(diǎn)C在⊙O上，連接AC，BC，若∠A=20°，∠B=70°，則∠ACB的度數(shù)為（ ）組卷：352引用：16難度：0.9 -
6．在同一坐標(biāo)系中，拋物線y=4x2，y=
x2，y=-14x2的共同特點(diǎn)是（ ）14組卷：958引用：32難度：0.9 -
7．拋物線y=-x2+bx+c上部分點(diǎn)的橫坐標(biāo)x,縱坐標(biāo)y的對(duì)應(yīng)值如下表：
從上表可知，下列說(shuō)法正確的個(gè)數(shù)是（ ）x … -2 -1 0 1 2 … y … 0 4 6 6 4 …
①拋物線與x軸的一個(gè)交點(diǎn)為（-2，0）；
②拋物線與y軸的交點(diǎn)為（0，6）；
③拋物線的對(duì)稱軸是直線x=1；
④在對(duì)稱軸左側(cè)y隨x增大而增大．組卷：1034引用：59難度：0.9 -
8．拋物線y=-x2+4x-4與坐標(biāo)軸的交點(diǎn)個(gè)數(shù)為（ ）
組卷：3695引用：32難度：0.9
三、解答題（共75分）
-
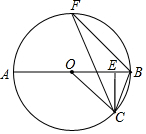23．已知，如圖，AB為⊙O的直徑，點(diǎn)C是半圓上一點(diǎn)，CE⊥AB于E，BF∥OC，連接BC，CF．
（1）求證：∠OCF=∠ECB；
（2）當(dāng)AB=10，BC=2，求CF的值．5組卷：406引用：5難度：0.4 -
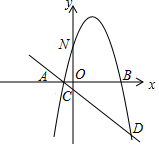24．如圖，拋物線y=-x2+bx+c與x軸交于A、B兩點(diǎn)（A在B的左側(cè)），與y軸交于點(diǎn)N，過(guò)A點(diǎn)的直線l：y=kx+n與y軸交于點(diǎn)C，與拋物線y=-x2+bx+c的另一個(gè)交點(diǎn)為D，已知A（-1，0），D（5，-6），P點(diǎn)為拋物線y=-x2+bx+c上一動(dòng)點(diǎn)（不與A、D重合）．
（1）求拋物線和直線l的解析式；
（2）當(dāng)點(diǎn)P在直線l上方的拋物線上時(shí)，過(guò)P點(diǎn)作PE∥x軸交直線l于點(diǎn)E，作PF∥y軸交直線l于點(diǎn)F，求PE+PF的最大值；
（3）設(shè)M為直線l上的點(diǎn)，探究是否存在點(diǎn)M，使得以點(diǎn)N、C，M、P為頂點(diǎn)的四邊形為平行四邊形？若存在，求出點(diǎn)M的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由．組卷：3732引用：17難度：0.4