2022-2023學(xué)年廣東省佛山市南海一中、獅山石門中學(xué)高一（下）月考數(shù)學(xué)試卷（3月份）

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．sin210°cos120°的值為（　　）

  A． 1 4

  B．- 3 4

  C．- 3 2

  D． 3 4
  組卷：254引用：11難度：0.9

  解析

• 2．已知向量

  a

  ，

  b

  ，則“|

  a

  |=|

  b

  |”是“

  a

  =±

  b

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：786引用：7難度：0.8

  解析

• 3．已知角α的終邊經(jīng)過點(diǎn)P（-8，m），且

  tanα

  =

  -

  3

  4

  ，則sinα的值是（　　）

  A． 3 5

  B． - 3 5

  C． - 4 5

  D． 4 5
  組卷：306引用：4難度：0.8

  解析

• 4．下列函數(shù)既是奇函數(shù)又是周期為π的函數(shù)是（　　）

  A．y=tan2x	B． y = sin （ 2 x + π 2 ）
  C．y=|sinx|	D． y = cos （ 3 2 π - 2 x ）
  組卷：290引用：7難度：0.7

  解析

• 5．在正方形ABCD中，E為AB的中點(diǎn)，F(xiàn)為CE的中點(diǎn)，則

  BF

  =（　　）

  A． 3 4 AB + 1 4 AD

  B． - 3 4 AB + 1 4 AD

  C． 1 2 AB + AD

  D． - 1 4 AB + 1 2 AD
  組卷：121引用：3難度：0.5

  解析

• 6．已知函數(shù)

  f

  （

  x

  ）

  =

  2

  sin

  （

  2

  x

  +

  π

  6

  ）

  ，則能夠使得y=2sinx變成函數(shù)f（x）的變換為（　　）

  A．先橫坐標(biāo)縮短到原來的 1 2 （縱坐標(biāo)不變），再向左平移 π 24 個(gè)單位長(zhǎng)度

  B．先橫坐標(biāo)伸長(zhǎng)到原來的2倍（縱坐標(biāo)不變），再向左平移 π 12 個(gè)單位長(zhǎng)度

  C．先向左平移 π 24 個(gè)單位長(zhǎng)度，再橫坐標(biāo)伸長(zhǎng)到原來的2倍（縱坐標(biāo)不變）

  D．先向左平移 π 6 個(gè)單位長(zhǎng)度，再橫坐標(biāo)縮短到原來的 1 2 （縱坐標(biāo)不變）
  組卷：58引用：3難度：0.7

  解析

• 7．在△ABC中，B=

  π

  4

  ，BC邊上的高等于

  1

  3

  BC，則cosA等于（　　）

  A． 3 10 10

  B． 10 10

  C．- 10 10

  D．- 3 10 10
  組卷：7982引用：68難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

• 21．已知函數(shù)

  f

  （

  x

  ）

  =

  sinx

  +

  1

  2

  sin

  2

  x

  ，該函數(shù)我們可以看作是函數(shù)y=sinx與

  y

  =

  1

  2

  sin

  2

  x

  相加，利用這兩個(gè)函數(shù)的性質(zhì)，我們可以探究f（x）的函數(shù)性質(zhì)．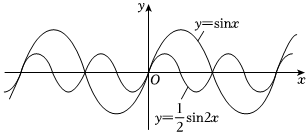
  
  （1）求出f（x）的最小正周期；
  （2）寫出f（x）的所有對(duì)稱中心（不需要說明理由）；
  （3）求使f（x）≥0成立的x的取值的集合．
  組卷：44引用：2難度：0.5

  解析

• 22．函數(shù)

  f

  （

  x

  ）

  =

  sin

  （

  ωx

  +

  π

  6

  ）

  +

  sin

  （

  ωx

  -

  π

  6

  ）

  -

  2

  co

  s

  2

  ωx

  2

  ，x∈R（其中ω＞0）．
  （1）求函數(shù)f（x）的最大值；
  （2）若函數(shù)f（x）的最小正周期為π，且關(guān)于x的方程

  f

  （

  x

  ）

  =

  1

  2

  在（0，π]有兩不等實(shí)數(shù)解x₁，x₂（x₁＜x₂），求sin（x₁-x₂）的值．
  組卷：57引用：2難度：0.6

  解析