2022-2023學(xué)年吉林省延邊州汪清四中高二（下）期末數(shù)學(xué)試卷

一、單項(xiàng)選擇題：本大題共8小題，每小題5分，共40分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的

• 1．已知集合A={x|-5＜x＜5}，B={-1，3，4，5}，則A∩B的子集的個(gè)數(shù)為（　　）

  A．2

  B．3

  C．8

  D．16
  組卷：191引用：3難度：0.9

  解析

• 2．已知x＞0，y＞0，x+y=1，則

  2

  x

  2

  -

  x

  +

  1

  xy

  的最小值為（　　）

  A．4

  B． 14 3

  C． 2 + 2

  D． 2 2 + 1
  組卷：791引用：5難度：0.7

  解析

• 3．已知函數(shù)f（x）=

  x

  -

  2

  ?

  x

  +

  5

  ，則函數(shù)的定義域?yàn)椋ā　。?/h2>

  A．{x|x≥-2}

  B．{x|x≥-5}

  C．{x|x≤5}

  D．{x|x≥2}
  組卷：929引用：6難度：0.9

  解析

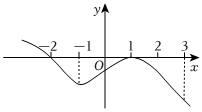• 4．已知函數(shù)f（x）的導(dǎo)函數(shù)f′（x）的圖象如圖所示，則下列結(jié)論中正確的是（　　）

  A．f（x）在區(qū)間（-2，3）上有2個(gè)極值點(diǎn)

  B．f（x）在x=-1處取得極小值

  C．f（x）在區(qū)間（-2，3）上單調(diào)遞減

  D．f（x）在x=1處取得極大值
  組卷：289引用：3難度：0.7

  解析

• 5．

  （

  x

  2

  -

  1

  2

  x

  ）

  5

  的展開式中x的系數(shù)是（　　）

  A．10

  B． - 5 2

  C． 5 4

  D． - 5 4
  組卷：383引用：6難度：0.8

  解析

• 6．弘揚(yáng)國(guó)學(xué)經(jīng)典，傳承中華文化，國(guó)學(xué)乃我中華民族五千年留下的智慧精髓，其中“五經(jīng)”是國(guó)學(xué)經(jīng)典著作，“五經(jīng)”指《詩(shī)經(jīng)》《尚書》《禮記》《周易》《春秋》．小明準(zhǔn)備學(xué)習(xí)“五經(jīng)”，現(xiàn)安排連續(xù)四天進(jìn)行學(xué)習(xí)且每天學(xué)習(xí)一種，每天學(xué)習(xí)的書都不一樣，其中《詩(shī)經(jīng)》與《禮記》不能安排在相鄰兩天學(xué)習(xí)，《周易》不能安排在第一天學(xué)習(xí)，則不同安排的方式有（　　）

  A．32種

  B．48種

  C．56種

  D．68種
  組卷：147引用：7難度：0.7

  解析

• 7．已知隨機(jī)變量X的分布列如表（其中a為常數(shù)），則下列計(jì)算結(jié)果正確的是（　　）
  

  X	0	1	2	3
  P	0.2	0.3	0.4	a

  A．a(chǎn)=0.2

  B．P（X≥2）=0.7

  C．E（X）=1.5

  D．D（X）=0.84
  組卷：194引用：3難度：0.8

  解析

四、解答題：本大題共6小題，共70分．解答應(yīng)寫出必要的文字說(shuō)明、證明過(guò)程或演算步驟

• 21．在今山西懷仁縣，故名．明《大明一統(tǒng)志》有“錦屏山在懷仁縣西南二十五里，山舊有磁窯”記載．懷仁陶瓷歷史已逾千年，始于春秋，興于遼金，盛于明清．目前懷仁有53家陶瓷企業(yè)，某陶瓷廠準(zhǔn)備燒制甲、乙、丙三件不同的工藝品，制作過(guò)程必須先后經(jīng)過(guò)兩次燒制，當(dāng)?shù)谝淮螣坪细窈蠓娇蛇M(jìn)入第二次燒制，兩次燒制過(guò)程相互獨(dú)立．根據(jù)該廠現(xiàn)有的技術(shù)水平，經(jīng)過(guò)第一次燒制后，甲、乙、丙三件產(chǎn)品合格的概率依次為0.5、0.6、0.4，經(jīng)過(guò)第二次燒制后，甲、乙、丙三件產(chǎn)品合格概率依次為0.6、0.5、0.75．
  （1）求第一次燒制后恰有一件產(chǎn)品合格的概率；
  （2）經(jīng)過(guò)前后兩次燒制后，記合格工藝品的件數(shù)為ξ，求隨機(jī)變量ξ的分布列及數(shù)學(xué)期望．
  組卷：90引用：3難度：0.5

  解析

• 22．4月23日是“世界讀書日”，讀書可以陶冶情操，提高人的思想境界，豐富人的精神世界，為了豐富校園生活，展示學(xué)生風(fēng)采，某中學(xué)在全校學(xué)生中開展了“閱讀半馬比賽”活動(dòng)．活動(dòng)要求每位學(xué)生在規(guī)定時(shí)間內(nèi)閱讀給定書目，并完成在線閱讀檢測(cè)．通過(guò)隨機(jī)抽樣，得到100名學(xué)生的檢測(cè)得分如表：
  

  	[40，50）	[50，60）	[60，70）	[70，80）	[80，90）	[90，100]
  男生	2	3	5	15	18	12
  女生	0	5	10	10	7	13

  （1）若檢測(cè)得分不低于70分的學(xué)生稱為“閱讀愛好者”，得分低于70分的學(xué)生稱為“非閱讀愛好者”．根據(jù)所給數(shù)據(jù)完成下列2×2列聯(lián)表；
  

  	閱讀愛好者	非閱讀愛好者	總計(jì)
  男生	_____	_____	_____
  女生	_____	_____	_____
  總計(jì)	_____	_____	_____

  （2）請(qǐng)根據(jù)所學(xué)知識(shí)判斷是否有95%的把握認(rèn)為“閱讀愛好者”與性別有關(guān)
  附：

  K

  2

  =

  n

  （

  ad

  -

  bc

  ）

  2

  （

  a

  +

  b

  ）

  （

  c

  +

  d

  ）

  （

  a

  +

  c

  ）

  （

  b

  +

  d

  ）

  ，其中n=a+b+c+d.
  

  P（K2≥k0）	0.05	0.025	0.010	0.005	0.001
  k0	3.841	5.024	6.635	7.879	10.828
  組卷：50引用：3難度：0.7

  解析