2022-2023學年廣西師大附中高二（上）期中數學試卷

一、單選題（8小題，共40.0分）

• 1．已知A（3，4，5），B（0，2，1），O（0，0，0），若

  OC

  =

  2

  5

  AB

  ，則C的坐標是（　　）

  A．（- 6 5 ，- 4 5 ，- 8 5 ）	B．（ 6 5 ，- 4 5 ，- 8 5 ）
  C．（- 6 5 ，- 4 5 ， 8 5 ）	D．（ 6 5 ， 4 5 ， 8 5 ）
  組卷：132引用：9難度：0.9

  解析

• 2．從甲地出發前往乙地，一天中有4趟汽車、3趟火車和1趟航班可供選擇．某人某天要從甲地出發，去乙地旅游，則所有不同走法的種數是（　　）

  A．16

  B．15

  C．12

  D．8
  組卷：64引用：5難度：0.8

  解析

• 3．若點P到點（0，2）的距離比它到直線y=-1的距離大1，則點P的軌跡方程為（　　）

  A．y2=4x

  B．x2=4y

  C．y2=8x

  D．x2=8y
  組卷：1312引用：4難度：0.8

  解析

• 4．直線ax+y-a=0（a∈R）與圓（x-2）²+y²=4的位置關系是（　　）

  A．相離

  B．相交

  C．相切

  D．無法確定
  組卷：116引用：8難度：0.7

  解析

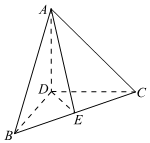• 5．如圖，在三棱錐A-BCD中，DA，DB，DC兩兩垂直，且DB=DC，E為BC中點，則

  AE

  ?

  BC

  等于（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：329引用：12難度：0.9

  解析

• 6．已知l₁：x+（m+1）y-2=0，l₂：mx+2y+4=0，則“m=1”是“l₁∥l₂”的（　　）條件．

  A．充分不必要	B．必要不充分
  C．充要條件	D．既不充分也不必要
  組卷：140引用：3難度：0.7

  解析

• 7．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左焦點為F，右頂點為A，直線x=a與雙曲線的一條漸近線的交點為B．若∠BFA=30°，則雙曲線的離心率為（　　）

  A． 2

  B． 3

  C．2

  D．3
  組卷：200引用：7難度：0.8

  解析

四、解答題（本大題共6小題，共72.0分。解答應寫出文字說明，證明過程或演算步驟）

• 21．圖1是直角梯形ABCD，AB∥CD，∠D=90°，AB=2，DC=3，

  AD

  =

  3

  ，

  CE

  =

  2

  ED

  ，以BE為折痕將△BCE折起，使點C到達C₁的位置，且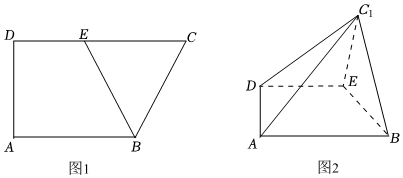

  A

  C

  1

  =

  6

  ，如圖2．
  
  （1）求證：平面BC₁E⊥平面ABED；
  （2）在棱DC₁上是否存在點P，使得C₁到平面PBE的距離為

  6

  2

  ？若存在，求出二平面P-BE-A的大小；若不存在，說明理由．
  組卷：229引用：7難度：0.4

  解析

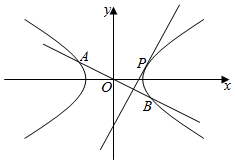• 22．在平面直角坐標系xOy中，已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的右焦點為（3，0），且經過點（2

  2

  ，1）．
  （1）求雙曲線C的標準方程；
  （2）已知A，B是雙曲線C上關于原點對稱的兩點，垂直于AB的直線l與雙曲線C有且僅有一個公共點P，當點P位于第一象限，且△PAB被x軸分割為面積比為3：2的兩部分時，求直線AB的方程．
  組卷：181引用：6難度：0.4

  解析