2020學年人教新版九年級上學期《第24章 圓》中考真題套卷（5）

一、選擇題（共10小題）

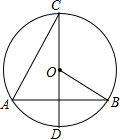• 1．如圖，在⊙O中，直徑CD⊥弦AB，則下列結論中正確的是（　　）

  A．AC=AB

  B．∠C= 1 2 ∠BOD

  C．∠C=∠B

  D．∠A=∠BOD
  組卷：6778引用：84難度：0.9

  解析

• 2．用反證法證明時，假設結論“點在圓外”不成立，那么點與圓的位置關系只能是（　　）

  A．點在圓內	B．點在圓上
  C．點在圓心上	D．點在圓上或圓內
  組卷：1067引用：11難度：0.9

  解析

• 3．如圖所示，矩形紙片ABCD中，AD=6cm,把它分割成正方形紙片ABFE和矩形紙片EFCD后，分別裁出扇形ABF和半徑最大的圓，恰好能作為一個圓錐的側面和底面，則AB的長為（　　）

  A．3.5cm

  B．4cm

  C．4.5cm

  D．5cm
  組卷：3355引用：20難度：0.8

  解析

• 4．如圖，在Rt△ABC中，∠C=90°，AC=4，BC=7，點D在邊BC上，CD=3，⊙A的半徑長為3，⊙D與⊙A相交，且點B在⊙D外，那么⊙D的半徑長r的取值范圍是（　　）

  A．1＜r＜4

  B．2＜r＜4

  C．1＜r＜8

  D．2＜r＜8
  組卷：1956引用：8難度：0.7

  解析

• 5．如圖，已知PA，PB是⊙O的兩條切線，A，B為切點，線段OP交⊙O于點M．給出下列四種說法：
  ①PA=PB；
  ②OP⊥AB；
  ③四邊形OAPB有外接圓；
  ④M是△AOP外接圓的圓心．
  其中正確說法的個數是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：4179引用：24難度：0.7

  解析

• 6．《九章算術》是我國古代第一部自成體系的數學專著，代表了東方數學的最高成就．它的算法體系至今仍在推動著計算機的發展和應用．書中記載：“今有圓材埋在壁中，不知大小，以鋸鋸之，深一寸，鋸道長一尺，問徑幾何？”譯為：“今有一圓柱形木材，埋在墻壁中，不知其大小，用鋸去鋸這木材，鋸口深1寸（ED=1寸），鋸道長1尺（AB=1尺=10寸）”，問這塊圓柱形木材的直徑是多少？”
  如圖所示，請根據所學知識計算：圓柱形木材的直徑AC是（　　）

  A．13寸

  B．20寸

  C．26寸

  D．28寸
  組卷：2751引用：15難度：0.7

  解析

• 7．如圖，拋物線y=

  1

  4

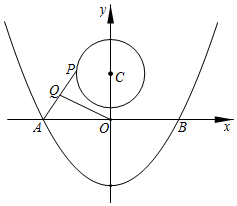  x²-4與x軸交于A、B兩點，P是以點C（0，3）為圓心，2為半徑的圓上的動點，Q是線段PA的中點，連接OQ，則線段OQ的最大值是（　　）

  A．3

  B． 41 2

  C． 7 2

  D．4
  組卷：7205引用：45難度：0.6

  解析

• 8．如圖，⊙O的直徑AB=6，若∠BAC=50°，則劣弧AC的長為（　　）

  A．2π

  B． 8 π 3

  C． 3 π 4

  D． 4 π 3
  組卷：2841引用：7難度：0.5

  解析

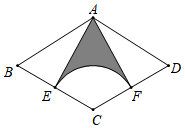• 9．如圖，在菱形ABCD中，點E是BC的中點，以C為圓心、CE為半徑作弧，交CD于點F，連接AE、AF．若AB=6，∠B=60°，則陰影部分的面積為（　　）

  A．9 3 -3π

  B．9 3 -2π

  C．18 3 -9π

  D．18 3 -6π
  組卷：6770引用：24難度：0.4

  解析

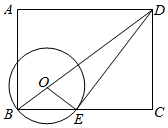• 10．如圖，在矩形ABCD中，AB=6，AD=8，點O在對角線BD上，以OB為半徑作⊙O交BC于點E，連接DE，若DE是⊙O的切線，此時⊙O的半徑為（　　）

  A．2

  B． 5 2

  C． 35 16

  D． 21 10
  組卷：2341引用：11難度：0.3

  解析

三、解答題（共10小題）

• 29．如圖，四邊形ABCD是矩形（AB＜BC），要在矩形ABCD內作一個以AB為邊的正方形ABEF，某位同學的作法如下：
  ①作∠ABC的平分線BM．BM交AD于點F；
  ②以點B為圓心，BA長為半徑畫弧，交BC于點E，連接EF．
  （1）求證：四邊形ABEF是正方形；
  （2）若AB=5，求圖中陰影部分的面積．
  組卷：210引用：5難度：0.5

  解析

• 30．如圖，已知△ABC，∠ACB=90°，AC＜BC，點D為AB的中點，過點D作BC的垂線，垂足為點F，過點A、C、D作⊙O交BC于點E，連接CD、DE．
  （1）求證：DF為⊙O的切線；
  （2）若AC=3，BC=9，求DE的長．
  組卷：1847引用：2難度：0.4

  解析