當前位置：試卷中心 > 試卷詳情

2021-2022學年福建省龍巖五中八年級（下）第一次月考數學試卷

發布：2024/11/10 0:0:2

一、選擇題（每小題4分，共40分）

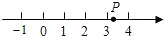1．如圖所示，數軸上點P所表示的可能是（　　）
A．
6
B．
10
C．
15
D．
31
組卷：205引用：31難度：0.9
解析
2．下列二次根式中，不能與
2
合并的是（　　）
A．
1
2
B．
8
C．
12
D．
18
組卷：3647引用：131難度：0.9
解析
3．下列各運算，正確的是（　　）
A．
-
3
×
（
-
12
）
=
6
B．
x
2
+
y
2
=
x
+
y
C．
（
-
2
）
2
=
-
2
D．
2
+
3
=
5
組卷：16引用：2難度：0.6
解析
4．如果
（
2
a
-
1
）
2
=1-2a,則（　　）
A．a＜
1
2
B．a≤
1
2
C．a＞
1
2
D．a≥
1
2
組卷：3090引用：112難度：0.9
解析
5．五根小木棒，其長度分別為7，15，20，24，25，現將它們擺成兩個直角三角形，如圖，其中正確的是（　　）
A． B． C． D．
組卷：3640引用：112難度：0.7
解析
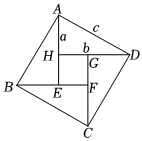6．如圖，四個全等的直角三角形與小正方形拼成的大正方形圖案，如果大正方形的面積為16，小正方形的面積為4，直角三角形的兩直角邊分別為a和b,那么（a+b）²的值為（　　）
A．25 B．28 C．16 D．48
組卷：51引用：1難度：0.6
解析
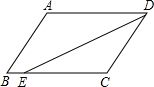7．如圖，在?ABCD中，已知AD=8cm,AB=6cm,DE平分∠ADC交BC邊于點E，則BE等于（　　）
A．2cm B．4cm C．6cm D．8cm
組卷：1524引用：116難度：0.9
解析
8．在下列條件中，能判定四邊形ABCD為平行四邊形的是（　　）
A．AB=AD，CB=CD B．AB∥CD，AD=BC
C．AB=CD，AD=BC D．∠A=∠B，∠C=∠D
組卷：84引用：7難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（9小題，共86分）

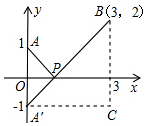24．閱讀材料：
例：說明代數式
x
2
+
1
+
（
x
-
3
）
2
+
4
的幾何意義，并求它的最小值．
解：
x
2
+
1
+
（
x
-
3
）
2
+
4
=
（
x
-
0
）
2
+
1
+
（
x
-
3
）
2
+
2
2
．
幾何意義：如圖，建立平面直角坐標系，點P（x,0）是x軸上一點，則
（
x
-
0
）
2
+
1
可以看成點P與點A（0，1）的距離，
（
x
-
3
）
2
+
2
2
可以看成點P與點B（3，2）的距離，所以原代數式的值可以看成線段PA與PB長度之和，它的最小值就是PA+PB的最小值．
求最小值：設點A關于x軸對稱點A′，則PA=PA′．因此，求PA+PB的最小值，只需求PA′+PB的最小值，而點A′，B間的直線段距離最短，所以PA′+PB的最小值為線段A′B的長度．為此，構造直角三角形A′CB，因為A′C=3，CB=3，所以由勾股定理得A'B=3
2
，即原式的最小值為3
2
．
根據以上閱讀材料，解答下列問題：
（1）代數式
（
x
-
1
）
2
+
1
+
（
x
-
2
）
2
+
9
的值可以看成平面直角坐標系中點P（x,0）與點A（1，1），點B
的距離之和．（填寫點B的坐標）
（2）代數式
x
2
+
49
+
x
2
-
12
x
+
37
的值可以看成平面直角坐標系中點P（x,0）與點A
、點B
的距離之和．（填寫點A，B的坐標）
（3）由①求出代數式
x
2
+
49
+
x
2
-
12
x
+
37
的最小值．
組卷：333引用：5難度：0.2
解析
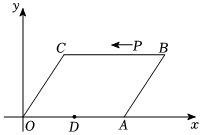25．如圖，在平面直角坐標系中，已知?OABC的頂點A（10，0）、C（2，4），點D是OA的中點，點P在BC上由點B向點C運動．
（1）求點B的坐標；
（2）若點P運動速度為每秒2個單位長度，點P運動的時間為t秒，當四邊形PCDA是平行四邊形時，求t的值；
（3）當△ODP是等腰三角形時，直接寫出點P的坐標．
組卷：597引用：6難度：0.4
解析