當前位置：試卷中心 > 試卷詳情

2023-2024學年江蘇省揚州市邗江中學高三（上）學情檢測數學試卷（10月份）

發布：2024/10/15 1:0:2

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．若集合M={x|y=
x
+lg（4-x）}，N={x|x²≤1}，則M∪N=（　　）
A．{x|0≤x＜4} B．{x|0≤x≤1} C．{x|-1≤x＜4} D．{x|1≤x＜4}
組卷：62引用：5難度：0.8
解析
2．在△ABC中，若b=2，A=60°，△ABC的面積為
2
3
，則a=（　　）
A．12 B．
2
3
C．2 D．4
組卷：345引用：5難度：0.8
解析
3．函數
y
=
（
1
2
）
-
x
2
+
x
+
2
的單調遞增區間是（　　）
A．
（
-
1
，
1
2
）
B．
（
-
∞
，
1
2
）
C．
（
1
2
，
+
∞
）
D．
（
1
2
，
2
）
組卷：290引用：3難度：0.7
解析
4．已知角α的頂點為坐標原點，始邊與x軸的非負半軸重合，終邊經過點P（-4，3），則
cos
（
3
π
2
-
2
α
）
=（　　）
A．
-
24
25
B．
-
7
25
C．
7
25
D．
24
25
組卷：81引用：1難度：0.8
解析
5．已知0＜m＜1，0＜n＜1，且2log₄m=log₂（1-n），則
1
m
+
9
n
的最小值是（　　）
A．18 B．16 C．10 D．4
組卷：220引用：7難度：0.7
解析
6．如圖，青銅器的上半部分可以近似看作圓柱體，下半部分可以近似看作兩個圓臺的組合體，已知AB=9cm,CD=3cm,則該青銅器的表面積為（　　）（假設上、下底面圓是封閉的）
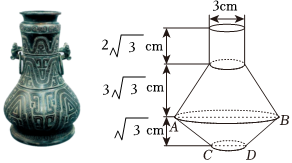
A．
（
36
3
+
81
）
π
2
c
m
2
B．
（
18
3
+
58
）
πc
m
2
C．
（
24
3
+
81
）
π
2
c
m
2
D．
（
18
3
+
36
）
πc
m
2
組卷：53引用：2難度：0.8
解析

7．已知函數
f
（
x
）
=
2
sin
（
ωx
+
φ
）
（
ω
＞
0
，
|
φ
|
＜
π
2
）
，其圖象相鄰的最高點之間的距離為π，將函數y=f（x）的圖象向左平移
π
12
個單位長度后函數為奇函數，則下列說法正確的是（　　）

A．f（x）的圖象關于直線

對稱

B．f（x）的圖象關于點

（

，

）

對稱

C．f（x）在

（

，-

）

上單調遞增

D．f（x）在區間（-a,a）上是增函數，則a的最大值為

組卷：29引用：1難度：0.7

解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟

21．一款擊鼓小游戲的規則如下：每盤游戲都需擊鼓三次，每次擊鼓后要么出現一次音樂，要么不出現音樂；每盤游戲擊鼓三次后，出現三次音樂獲得150分，出現兩次音樂獲得100分，出現一次音樂獲得50分，沒有出現音樂則獲得-300分．設每次擊鼓出現音樂的概率為
p
（
0
＜
p
＜
2
5
）
，且各次擊鼓出現音樂相互獨立．
（1）若一盤游戲中僅出現一次音樂的概率為f（p），求f（p）的最大值點p₀；
（2）以（1）中確定的p₀作為p的值，玩3盤游戲，出現音樂的盤數為隨機變量X，求每盤游戲出現音樂的概率p₁，及隨機變量X的期望EX；
（3）玩過這款游戲的許多人都發現，若干盤游戲后，與最初的分數相比，分數沒有增加反而減少了．請運用概率統計的相關知識分析分數減少的原因．
組卷：472引用：7難度：0.5
解析
22．青島膠東國際機場的顯著特點之一是彎曲曲線的運用，衡量曲線彎曲程度的重要指標是曲率，曲線的曲率定義如下：若f′（x）是f（x）的導函數，f″（x）是f′（x）的導函數，則曲線y=f（x）在點（x,f（x））處的曲率K=
|
f
″
（
x
）
|
（
1
+
[
f
′
（
x
）
]
2
）
3
2
．
已知函數f（x）=ae^x-lnx-bcos（x-1）（a≥0，b＞0），若a=0，則曲線y=f（x）在點（1，f（1））處的曲率為
2
2
．

（1）求b；
（2）若函數f（x）存在零點，求a的取值范圍；
（3）已知1.098＜ln3＜1.099，e^0.048＜1.050，e^-0.045＜0.956，證明：1.14＜lnπ＜1.15．
組卷：401引用：4難度：0.1
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（ 36 3 + 81 ） π 2 c m 2	B．（ 18 3 + 58 ） πc m 2
C．（ 24 3 + 81 ） π 2 c m 2	D．（ 18 3 + 36 ） πc m 2

2023-2024學年江蘇省揚州市邗江中學高三（上）學情檢測數學試卷（10月份）

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．若集合M={x|y=x+lg（4-x）}，N={x|x2≤1}，則M∪N=（ ）

2．在△ABC中，若b=2，A=60°，△ABC的面積為23，則a=（ ）

3．函數y=（12）-x2+x+2的單調遞增區間是（ ）

4．已知角α的頂點為坐標原點，始邊與x軸的非負半軸重合，終邊經過點P（-4，3），則cos（3π2-2α）=（ ）

5．已知0＜m＜1，0＜n＜1，且2log4m=log2（1-n），則1m+9n的最小值是（ ）

6．如圖，青銅器的上半部分可以近似看作圓柱體，下半部分可以近似看作兩個圓臺的組合體，已知AB=9cm,CD=3cm,則該青銅器的表面積為（ ）（假設上、下底面圓是封閉的）

7．已知函數f（x）=2sin（ωx+φ）（ω＞0，|φ|＜π2），其圖象相鄰的最高點之間的距離為π，將函數y=f（x）的圖象向左平移π12個單位長度后函數為奇函數，則下列說法正確的是（ ）

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟

1．若集合M={x|y=
x
+lg（4-x）}，N={x|x²≤1}，則M∪N=（　　）

2．在△ABC中，若b=2，A=60°，△ABC的面積為
2
3
，則a=（　　）

3．函數
y
=
（
1
2
）
-
x
2
+
x
+
2
的單調遞增區間是（　　）

4．已知角α的頂點為坐標原點，始邊與x軸的非負半軸重合，終邊經過點P（-4，3），則
cos
（
3
π
2
-
2
α
）
=（　　）

5．已知0＜m＜1，0＜n＜1，且2log₄m=log₂（1-n），則
1
m
+
9
n
的最小值是（　　）

6．如圖，青銅器的上半部分可以近似看作圓柱體，下半部分可以近似看作兩個圓臺的組合體，已知AB=9cm,CD=3cm,則該青銅器的表面積為（　　）（假設上、下底面圓是封閉的）

7．已知函數
f
（
x
）
=
2
sin
（
ωx
+
φ
）
（
ω
＞
0
，
|
φ
|
＜
π
2
）
，其圖象相鄰的最高點之間的距離為π，將函數y=f（x）的圖象向左平移
π
12
個單位長度后函數為奇函數，則下列說法正確的是（　　）