2022-2023學(xué)年廣東省廣州二中南沙分校九年級(jí)（上）期末數(shù)學(xué)試卷

一、選擇題（每小題3分，共10小題，共30分）

• 1．下列圖形是中心對(duì)稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：97引用：6難度：0.9

  解析

• 2．下列方程中，是一元二次方程的是（　　）

  A．3x2-5x=0

  B．2x+1=0

  C．y-3x=0

  D．2x3-1=0
  組卷：74引用：2難度：0.8

  解析

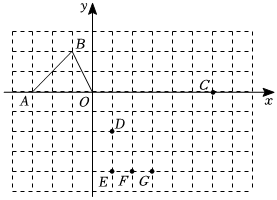• 3．如圖，在平面直角坐標(biāo)系中，以點(diǎn)O為位似中心，把△AOB擴(kuò)大后得到△COM，使得△AOB∽△COM，則點(diǎn)M與圖中的（　　）重合．

  A．點(diǎn)D

  B．點(diǎn)E

  C．點(diǎn)F

  D．點(diǎn)G
  組卷：54引用：1難度：0.7

  解析

• 4．把拋物線y=4（x+1）²-3的圖象通過怎樣平移可以得到拋物線y=4x²的圖象（　　）

  A．先向上平移1個(gè)單位長(zhǎng)度，再向右平移3個(gè)單位長(zhǎng)度

  B．先向下平移1個(gè)單位長(zhǎng)度，再向左平移3個(gè)單位長(zhǎng)度

  C．先向上平移3個(gè)單位長(zhǎng)度，再向右平移1個(gè)單位長(zhǎng)度

  D．先向上平移3個(gè)單位長(zhǎng)度，再向左平移1個(gè)單位長(zhǎng)度
  組卷：130引用：1難度：0.5

  解析

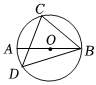• 5．如圖，AB為⊙O的直徑．C，D是圓周上的兩點(diǎn)，若∠ABC=48°，則銳角∠BDC的度數(shù)為（　　）

  A．47°

  B．42°

  C．48°

  D．36°
  組卷：194引用：2難度：0.8

  解析

• 6．若點(diǎn)A（-2，y₁）．B（-1，y₂），C（2，y₃）在反比例函數(shù)y=-

  4

  x

  的圖象上，則y₁，y₂，y₃的大小關(guān)系是（　　）

  A．y1＞y2＞y3

  B．y2＞y3＞y1

  C．y3＞y2＞y1

  D．y2＞y1＞y3
  組卷：211引用：4難度：0.5

  解析

• 7．已知有一個(gè)亭子，它的地基是半徑為4m的正六邊形，則此地基的周長(zhǎng)為（　　）

  A．12m

  B．12 3 m

  C．24m

  D．24 3 m
  組卷：133引用：1難度：0.6

  解析

• 8．小元設(shè)計(jì)了一個(gè)魔術(shù)盒，當(dāng)任意實(shí)數(shù)對(duì)（m,n）進(jìn)入其中時(shí)，會(huì)得到一個(gè)新的實(shí)數(shù)m²+2n-7，例如把（3，-2）放入其中，就會(huì)得到3²+2×（-2）-7=-2．現(xiàn)將實(shí)數(shù)對(duì)（a,-4a）放入其中，得到實(shí)數(shù)-23，則二次函數(shù)y=ax²-8x+5的最值為（　　）

  A．-1

  B．1

  C．4

  D．9
  組卷：147引用：1難度：0.5

  解析

三、解答題（共8小題，滿分72分，解答應(yīng)寫出文字說明、證明過程或演算步驟.）

• 23．定義：若關(guān)于x的一元二次方程ax²+bx+c=0（a≠0）的兩個(gè)實(shí)數(shù)根為x₁，x₂（x₁＜x₂），以x₁，x₂為橫坐標(biāo)和縱坐標(biāo)
  得到點(diǎn)M（x₁，x₂），則稱點(diǎn)M為該一元二次方程的衍生點(diǎn)．
  （1）若一元二次方程為x²+2x=0，請(qǐng)直接寫出該方程的衍生點(diǎn)M的坐標(biāo)為

  ．
  （2）若關(guān)于x的一元二次方程為x²-2（m+1）x+m²+2m=0
  ①求證：不論m為何值，該方程總有兩個(gè)不相等的實(shí)數(shù)根：并求出該方程的衍生點(diǎn)M的坐標(biāo)：
  ②直線l₁：y=-x+5與x軸交于點(diǎn)A，直線l過點(diǎn)B（-1，0），且與l₂相交于點(diǎn)C（1，4）．若由①得到的點(diǎn)M在△ABC的內(nèi)部，求m的取值范圍；
  （3）是否存在b,c,使得不論k（k≠0）為何值，關(guān)于x的方程x²+bx+c=0的衍生點(diǎn)M始終在直線y=-kx+2（4+k）的圖象上．若有，請(qǐng)直接寫出b,c的值；若沒有，請(qǐng)說明理由．
  組卷：532引用：2難度：0.5

  解析

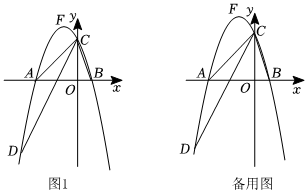• 24．在平面直角坐標(biāo)系xOy中，拋物線y=ax²+2ax-3a與x軸交于A、B兩點(diǎn)（點(diǎn)A在點(diǎn)B的左側(cè)），與y軸交于點(diǎn)C，OC=3OB．
  （1）分別求A和B的坐標(biāo)及a的值；
  （2）如圖1，點(diǎn)D在第三象限的拋物線上，分別連接BC、AC、CD，若∠BCO=∠ACD，求直線CD的解析式：
  （3）在（2）的條件下，CD交對(duì)稱軸l于點(diǎn)M，作直線m∥CD，請(qǐng)求出滿足使直線m是半徑為

  3

  5

  5

  的圓O的切線的解析式．
  組卷：172引用：1難度：0.4

  解析