2022-2023學(xué)年廣東省深圳外國(guó)語(yǔ)學(xué)校高二（下）期末數(shù)學(xué)試卷

一、單選題：本題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

• 1．已知集合A={1，3，a²}，B={1，a+2}，A∪B=A，則實(shí)數(shù)a的值為（　　）

  A．{2}

  B．{-1，2}

  C．{1，2}

  D．{0，2}
  組卷：741引用：7難度：0.7

  解析

• 2．設(shè)z是復(fù)數(shù)且|z-1+2i|=1，則|z|的最小值為（　　）

  A．1

  B． 3 - 1

  C． 5 - 1

  D． 5
  組卷：165引用：5難度：0.8

  解析

• 3．在平面直角坐標(biāo)系中，已知點(diǎn)P（3，4）為角α終邊上一點(diǎn)，若cos（α+β）=

  1

  3

  ，β∈（0，π），則cosβ=（　　）

  A． 3 - 8 2 15

  B． 3 + 8 2 15

  C． 4 + 6 2 15

  D． 6 2 - 4 15
  組卷：430引用：6難度：0.7

  解析

• 4．已知圓臺(tái)的上、下底面圓的半徑之比為

  1

  2

  ，側(cè)面積為9π，在圓臺(tái)的內(nèi)部有一球O，該球與圓臺(tái)的上、下底面及母線均相切，則球O的表面積為（　　）

  A．3π

  B．5π

  C．8π

  D．9π
  組卷：407引用：7難度：0.7

  解析

• 5．設(shè)

  a

  ，

  b

  為單位向量，

  a

  在

  b

  方向上的投影向量為-

  1

  2

  b

  ，則|

  a

  -2

  b

  |=（　　）

  A． 2

  B． 3

  C． 5

  D． 7
  組卷：1118引用：19難度：0.7

  解析

• 6．為了貫徹落實(shí)《中共中央國(guó)務(wù)院關(guān)于深入打好污染防治攻堅(jiān)戰(zhàn)的意見》，某造紙企業(yè)的污染治理科研小組積極探索改良工藝，使排放的污水中含有的污染物數(shù)量逐漸減少．已知改良工藝前所排放廢水中含有的污染物數(shù)量為2.65g/m³，首次改良工藝后排放的廢水中含有的污染物數(shù)量為2.59g/m³，第n次改良工藝后排放的廢水中含有的污染物數(shù)量r_n滿足函數(shù)模型

  r

  n

  =

  r

  0

  +

  （

  r

  1

  -

  r

  0

  ）

  ?

  5

  0

  .

  25

  n

  +

  p

  （

  p

  ∈

  R

  ，

  n

  ∈

  N

  *

  ）

  ，其中r₀為改良工藝前所排放的廢水中含有的污染物數(shù)量，r₁為首次改良工藝后所排放的廢水中含有的污染物數(shù)量，n為改良工藝的次數(shù)．假設(shè)廢水中含有的污染物數(shù)量不超過(guò)0.25g/m³時(shí)符合廢水排放標(biāo)準(zhǔn)，若該企業(yè)排放的廢水符合排放標(biāo)準(zhǔn)，則改良工藝的次數(shù)最少要（參考數(shù)據(jù)：lg2≈0.301）（　　）

  A．8次

  B．9次

  C．10次

  D．11次
  組卷：90引用：2難度：0.5

  解析

• 7．設(shè)實(shí)數(shù)x＞1，y∈R，e為自然對(duì)數(shù)的底數(shù)，若exlnx+e^y＜ye^y，則（　　）

  A．eylnx＞e

  B．eylnx＜e

  C．ey＞ex

  D．ey＜ex
  組卷：904引用：9難度：0.3

  解析

四、解答題：本題共6小題，共70分．解答題應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟．

• 21．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  2

  2

  ，過(guò)點(diǎn)

  （

  -

  1

  ，

  2

  2

  ）

  ．
  （1）求橢圓C的標(biāo)準(zhǔn)方程；
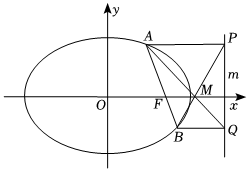
  （2）設(shè)橢圓的右焦點(diǎn)為F，定直線m：x=2，過(guò)點(diǎn)F且斜率不為零的直線l與橢圓交于A，B兩點(diǎn)，過(guò)A，B兩點(diǎn)分別作AP⊥m于P，BQ⊥m于Q，直線AQ、BP交于點(diǎn)M，證明：M點(diǎn)為定點(diǎn)，并求出M點(diǎn)的坐標(biāo)．
  組卷：238引用：2難度：0.5

  解析

• 22．已知函數(shù)f（x）=

  cosx

  -

  x

  x

  2

  ，x∈（0，+∞）．
  （1）證明：函數(shù)f（x）在（0，+∞）上有且只有一個(gè)零點(diǎn)；
  （2）當(dāng)x∈（0，π）時(shí)，求函數(shù)f（x）的最小值；
  （3）設(shè)g_i（x）=k_ix+b,i=1，2，若對(duì)任意的x∈[

  π

  2

  ，+∞），g₁（x）≤f（x）≤g₂（x）恒成立，且不等式兩端等號(hào)均能取到，求k₁+k₂的最大值．
  組卷：271引用：5難度：0.4

  解析