2022-2023學年湖南省邵陽市新邵縣七年級（下）期末數學試卷

一、選擇題（每小題3分，共30分）

• 1．下列計算正確的是（　　）

  A．a2?a3=a6	B．（x3）2=x5
  C．（2a）2=4a2	D．（x+1）2=x2+1
  組卷：118引用：2難度：0.6

  解析

• 2．第24屆冬季奧林匹克運動會將于2022年2月4日至2月20日在中國北京市和張家口市聯合舉辦．以下是歷屆的冬奧會會徽設計的部分圖形，其中不是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：121引用：5難度：0.9

  解析

• 3．若二元一次方程組

  2 x + y = 3

  3 x - y = 2

  的解同時也是方程2x-my=-1的解，那么m的值為（　　）

  A．-2

  B．-1

  C．3

  D．4
  組卷：619引用：18難度：0.7

  解析

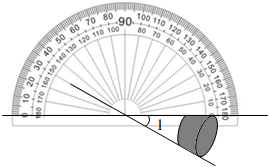• 4．如圖，利用工具測量角，則∠1的大小為（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：1587引用：42難度：0.7

  解析

• 5．下列各組式子中，沒有公因式的是（　　）

  A．-a2+ab與ab2-a2b	B．mx+y與x+y
  C．（a+b）2與-a-b	D．5m（x-y）與y-x
  組卷：1111引用：11難度：0.9

  解析

• 6．多項式x²+x-6可因式分解成（x+a）（x+b），其中a、b均為整數，則（a+b）²⁰²³的值為（　　）

  A．-1

  B．1

  C．-2023

  D．2023
  組卷：302引用：2難度：0.8

  解析

• 7．如圖，在三角形ABC中，點E，D，F分別在AB，BC，AC上，連接ED，CE，EF，下列條件中，能推理出DE∥AC的是（　　）

  A．∠EDC=∠EFC

  B．∠AFE=∠ACD

  C．∠DEC=∠ECF

  D．∠FEC=∠BCE
  組卷：1277引用：8難度：0.6

  解析

• 8．2023年4月23日是第28個世界讀書日，某校舉行了演講大賽，演講得分按“演講內容”占40%、“語言表達”占40%、“形象風度”占10%、“整體效果”占10%進行計算，小芳這四項的得分依次為86，88，90，94，則她的最后得分是（　　）

  A．86分

  B．88分

  C．90分

  D．94分
  組卷：199引用：6難度：0.6

  解析

三、解答題（本大題共7小題，第19、21、22題每小題8分，第20、23、24題每小題8分，第25題12分，共66分）

• 24．某校舉辦“歌唱祖國”演唱比賽，十位評委對每位同學的演唱進行現場打分，對參加比賽的甲、乙、丙三位同學得分的數據進行整理、描述和分析，下面給出了部分信息．
  ?a.甲、乙兩位同學得分的折線圖；
  b.丙同學得分：10，10，10，9，9，8，3，9，8，10
  c.甲、乙、丙三位同學得分的平均數：
  

  同學	甲	乙	丙
  平均數	8.6	8.6	m

  根據以上信息，回答下列問題：
  （1）求表中m的值；
  （2）如果每位同學的最后得分為去掉十位評委打分中的一個最高分和一個最低分后的平均分，最后得分越高，則認為該同學表現越優秀．據此推斷：在甲、乙、丙三位同學中，表現最優秀的是哪一位？
  （3）在參加比賽的同學中，如果某同學得分的10個數據的方差越小，則認為評委對該同學演唱的評價越一致．據此推斷：甲、乙兩位同學中，評委對誰的評價更一致？
  組卷：30引用：1難度：0.7

  解析

• 25．如圖1，點A，O，B依次在直線MN上，現將射線OA繞點O沿順時針方向以每秒4°的速度轉動，同時射線OB繞點O沿逆時針方向以每秒6°的速度轉動，直線MN保持不動，如圖2．設轉動時間為t（0≤t≤60，單位：秒）
  ?
  （1）當t=5時，求∠AOB的度數；
  （2）在轉動過程中，當∠AOB 第二次達到60°時，求t的值；
  （3）在轉動過程中是否存在這樣的t,使得射線OB與射線OA垂直？如果存在，請求出t的值；如果不存在，請說明理由．
  組卷：195引用：1難度：0.4

  解析