2021-2022學年山東省德州市夏津縣萬隆實驗中學八年級（下）期中數學試卷

一、選擇題（每小題4分，共48分）

• 1．若

  x

  ?

  x

  -

  6

  =

  x

  （

  x

  -

  6

  ）

  ，則（　　）

  A．x≥6	B．x≥0
  C．0≤x≤6	D．x為一切實數
  組卷：1985引用：55難度：0.9

  解析

• 2．下列各組數中，能構成直角三角形的是（　　）

  A．4，5，7

  B．1，2， 5

  C．6，8，11

  D．5，12，23
  組卷：229引用：10難度：0.8

  解析

• 3．下列各式中，屬于最簡二次根式的是（　　）

  A． 1 2

  B． 4

  C． 5

  D． 12
  組卷：223引用：9難度：0.8

  解析

• 4．已知平行四邊形ABCD中，∠B=4∠A，則∠C=（　　）

  A．18°

  B．36°

  C．72°

  D．144°
  組卷：1285引用：51難度：0.9

  解析

• 5．下列說法錯誤的是（　　）

  A．若△ABC中，a2=（b+c）（b-c），則△ABC是直角三角形

  B．若△ABC中，a2+b2≠c2，則△ABC不是直角三角形

  C．若△ABC中，a：b：c=13：5：12，則∠A=90°

  D．若△ABC中，a、b、c三邊的長分別為n2-1、2n、n2+1（n＞1），則△ABC是直角三角形
  組卷：226引用：3難度：0.9

  解析

• 6．以下各式中計算正確的是（　　）

  A．- （ - 6 ） 2 =-6

  B．（- 3 ）2=-3

  C． （ - 16 ） 2 =±16

  D． a 2 =a
  組卷：100引用：3難度：0.9

  解析

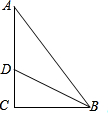• 7．如圖，在Rt△ABC中，∠C=90°，D為AC上一點，且DA=DB=5，又△DAB的面積為10，那么DC的長是（　　）

  A．4

  B．3

  C．5

  D．4.5
  組卷：577引用：10難度：0.7

  解析

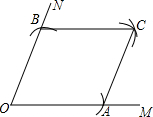• 8．如圖，以O為圓心，OA長為半徑畫弧分別交OM、ON于A、B兩點，再分別以A、B為圓心，以OA長為半徑畫弧，兩弧交于點C，分別連接AC、BC，則四邊形OACB一定是（　　）

  A．梯形

  B．菱形

  C．矩形

  D．正方形
  組卷：696引用：7難度：0.9

  解析

三、解答題（共78分）

• 24．勾股定理是一個基本的幾何定理，早在我國西漢時期算書《周髀算經》就有“勾三股四弦五”的記載．如果一個直角三角形三邊長都是正整數，這樣的直角三角形叫做“整數直角三角形”；這三個整數叫做一組“勾股數”．在一次“構造勾股數”的探究性學習中，老師給出了下表：
  

  m	2	3	3	4	…
  n	1	1	2	3	…
  a	22+12	32+12	32+22	42+32	…
  b	4	6	12	24	…
  c	22-12	32-12	32-22	42-32	…

  其中m、n為正整數，且m＞n.
  （1）觀察表格，當m=2，n=1時，此時對應的a、b、c的值能否為直角三角形三邊的長？說明你的理由．
  （2）探究a,b,c與m、n之間的關系并用含m、n的代數式表示：a=

  ，b=

  ，c=

  ．
  （3）以a,b,c為邊長的三角形是否一定為直角三角形？如果是，請說明理由；如果不是，請舉出反例．
  組卷：211引用：8難度：0.6

  解析

• 25．如圖，Rt△ABC中，∠B=90°，AC=30cm,∠C=30°，點D從點C出發沿CA方向以2cm/秒的速度向點A勻速運動，同時點E從點A出發沿AB方向以1cm/秒的速度向點B勻速運動，當其中一個點到達終點時，另一個點也隨之停止運動．設點D、E運動的時間是t秒（0＜t≤15）．過點D作DF⊥BC于點F，連接DE、EF．
  （1）求證：AE=DF；
  （2）四邊形AEFD能夠成為菱形嗎？如果能，求出相應的t值；如果不能，請說明理由；
  （3）當t為何值時，△DEF為直角三角形？請說明理由．
  組卷：650引用：10難度：0.3

  解析