2023-2024學年江蘇省南通市崇川區通州區高二（上）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．在空間直角坐標系中，點A（9，8，5）關于xOz平面對稱的點的坐標為（　　）

  A．（9，8，-5）

  B．（9，-8，5）

  C．（-9，8，5）

  D．（-9，8，-5）
  組卷：13引用：1難度：0.8

  解析

• 2．直線

  x

  4

  +

  y

  2

  =

  1

  的一個方向向量是（　　）

  A．（1，2）

  B．（1，-2）

  C．（-2，1）

  D．（-2，-1）
  組卷：32引用：1難度：0.7

  解析

• 3．已知在三棱錐P-ABC中，M，N分別是PC和AB的中點．設

  PA

  =

  a

  ，

  PB

  =

  b

  ，

  PC

  =

  c

  ，則

  MN

  =（　　）

  A． a + b - 1 2 c	B． a + 1 2 b - 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． - 1 2 a - 1 2 b + 1 2 c
  組卷：23引用：1難度：0.7

  解析

• 4．已知橢圓C：

  x

  2

  3

  -

  k

  +

  y

  2

  5

  +

  k

  =

  1

  的焦點在y軸上，則實數k的取值范圍是（　　）

  A．（-1，3）	B．（-5，-1）
  C．（-5，3）	D．（-5，-1）∪（-1，3）
  組卷：93引用：4難度：0.7

  解析

• 5．圓C：x²+y²+2x-4y-4=0關于直線x-y-1=0對稱的圓的方程是（　　）

  A．（x-3）2+（y+2）2=3	B．（x-3）2+（y+2）2=9
  C．（x+3）2+（y-2）2=3	D．（x+3）2+（y-2）2=9
  組卷：1102引用：4難度：0.5

  解析

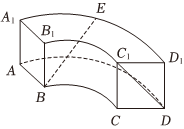• 6．中國古代數學瑰寶《九章算術》中記載了一種稱為“曲池”的幾何體，該幾何體為上、下底面均為扇環形的柱體（扇環是指圓環被扇形截得的部分）．現有一個如圖所示的曲池，其中AA₁⊥底面ABCD，底面扇環所對的圓心角為

  2

  π

  3

  ，扇環對應的兩個圓的半徑之比為1：2，AB=1，AA₁=1，E是

  ?

  A

  1

  D

  1

  的中點，則異面直線BE與C₁D所成角的余弦值為（　　）

  A． 2 4

  B． 2 8

  C． 5 2 8

  D． 2 5 5
  組卷：107引用：5難度：0.6

  解析

• 7．已知橢圓C：

  x

  2

  12

  +

  y

  2

  8

  =

  1

  的左焦點為F，P為C上一動點，定點

  A

  （

  -

  1

  ，

  3

  ）

  ，則|PF|+|PA|的最大值為（　　）

  A． 4 3

  B． 6 3

  C． 2 + 2 3

  D． 2 + 4 3
  組卷：369引用：5難度：0.6

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

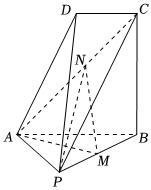• 21．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，AB∥CD，AB⊥BC，PA=AB=BC=2，CD=1，M是PB的中點，點N在線段AC上．
  （1）當N是AC中點時，求點N到平面PCD的距離；
  （2）當二面角A-MN-P的正弦值為

  7

  3

  時，求

  AN

  AC

  的值．
  組卷：133引用：1難度：0.3

  解析

• 22．在平面直角坐標系xOy中，已知圓O：x²+y²=1，點F（2，0），以線段FG為直徑的圓與圓O相切，記動點G的軌跡為W．
  （1）求W的方程；
  （2）設點M在x軸上，點N（0，1），在W上是否存在兩點A，B，使得當A，B，N三點共線時，△ABM是以AB為斜邊的等腰直角三角形？若存在，求出點M的坐標和直線AB的方程；若不存在，請說明理由．
  組卷：79引用：3難度：0.5

  解析