2020-2021學年重慶市青木關中學高二（上）期中數學試卷

一、單選題（本題共8個小題，每小題5分，共40分）

• 1．若直線l的一個方向向量為（-1，

  3

  ），則它的傾斜角為（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：519引用：28難度：0.8

  解析

• 2．已知圓C：x²+y²-2x+4y=0關于直線3x-2ay-11=0對稱，則實數a的值為（　　）

  A．-2

  B．2

  C．3

  D．4
  組卷：63引用：2難度：0.8

  解析

• 3．若點P（3，-1）是圓（x-2）²+y²=25的弦AB的中點，則直線AB的方程為（　　）

  A．x+y-2=0

  B．2x-y-7=0

  C．x-y-4=0

  D．2x+y-5=0
  組卷：344引用：8難度：0.9

  解析

• 4．過點A（3，5）作圓（x-2）²+（y-3）²=1的切線，則切線的方程為（　　）

  A．x=3或3x+4y-29=0	B．y=3或3x+4y-29=0
  C．x=3或3x-4y+11=0	D．y=3或3x-4y+11=0
  組卷：190引用：4難度：0.7

  解析

• 5．已知向量

  n

  =（2，0，1）為平面α的法向量，點A（-1，2，1）在α內，則P（1，2，2）到α的距離為（　　）

  A． 5 5

  B． 5

  C．2 5

  D． 5 10
  組卷：183引用：14難度：0.9

  解析

• 6．在棱長為1的正方體ABCD-A₁B₁C₁D₁中，點E為底面A₁B₁C₁D₁內一動點，則

  EA

  ?

  EC

  的取值范圍是 （　　）

  A．[ 1 2 ，1]

  B．[0，1]

  C．[-1，0]

  D．[- 1 2 ，0]
  組卷：148引用：9難度：0.6

  解析

• 7．已知直線3x+4y-15=0與圓x²+y²=25交于A、B兩點，點C在圓O上，且S_△ABC=8，則滿足條件的點C的個數為（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：200引用：7難度：0.9

  解析

四、解答題（本大題6個大題，共70分，解答應寫出文字說明，證明過程或演算步驟）

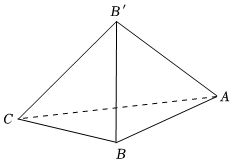• 21．如圖，將等腰直角△ABC沿斜邊AC旋轉，使得B到達B'的位置，且BB'=AB．
  （1）證明：平面AB'C⊥平面ABC．
  （2）求直線CB'與平面ABB′所成角的正弦值．
  （3）若在棱CB'上存在點M，使得

  CM

  =μ

  CB

  ′

  ，

  μ

  ∈

  [

  1

  5

  ，

  4

  5

  ]

  ，在棱BB'上存在點N，使得

  BN

  =λ

  BB

  ′

  ，且BM⊥AN，求λ的取值范圍．
  組卷：6引用：1難度：0.5

  解析

• 22．已知圓C的圓心在第一象限內，圓C關于直線y=3x對稱，與x軸相切，被直線y=x截得的弦長為2

  7

  ．
  （1）求圓C的方程；
  （2）若點P在直線x+y+1=0上運動，過點P作圓C的兩條切線PA、PB，切點分別為A，B點．
  ①求四邊形PACB面積的最小值；
  ②直線AB是否過定點？若AB過定點，求此定點坐標；若不過定點，請說明．
  組卷：43引用：1難度：0.5

  解析