2022-2023學年四川省眉山市仁壽一中南校區高二（下）月考數學試卷（文科）（3月份）

一、選擇題：本題共12小題，每小題5分，在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．下列與二進制數1001101_（2）相等的是（　　）

  A．115（8）

  B．114（8）

  C．113（8）

  D．116（8）
  組卷：120引用：6難度：0.8

  解析

• 2．已知回歸直線的斜率的估計值為1.23，樣本點的中心為（4，5），則回歸直線方程為（　　）

  A． ? y = 1 . 23 x + 4	B． ? y = 1 . 23 x + 5
  C． ? y = 1 . 23 x + 0 . 08	D． ? y =0.08x+1.23
  組卷：469引用：120難度：0.9

  解析

• 3．已知100件產品中有5件次品，從這100件產品任意取出3件，設A表示事件“3件產品全不是次品”，B表示事件“3件產品全是次品”，C表示事件“3件產品中至少有1件次品”，則下列結論正確的是（　　）

  A．B與C互斥

  B．A與C互斥

  C．A、B、C任意兩個事件均互斥

  D．A、B、C任意兩個事件均不互斥
  組卷：41引用：4難度：0.8

  解析

• 4．某班統計一次數學測驗成績的平均分與方差，計算完畢才發現有個同學的分數還未錄入，只好重算一次．已知原平均分和原方差分別為

  x

  ，

  s

  2

  ?，新平均分和新方差分別為

  x

  1

  ，

  s

  2

  1

  ?，若此同學的得分恰好為

  x

  ?，則（　　）

  A． x = x 1 ， s 2 = s 2 1 ?	B． x = x 1 ， s 2 ＜ s 2 1 ?
  C． x = x 1 ， s 2 ＞ s 2 1 ?	D． x ＜ x 1 ， s 2 = s 2 1 ?
  組卷：169引用：9難度：0.8

  解析

• 5．某校有高三學生1200名，現采用系統抽樣法從中抽取200名學生進行核酸檢測，用電腦對這1200名學生隨機編號1，2，3，…，1200，已知隨機抽取的一個學生編號為10，則抽取的學生最大編號為（　　）

  A．2004

  B．1198

  C．1192

  D．1086
  組卷：67引用：6難度：0.7

  解析

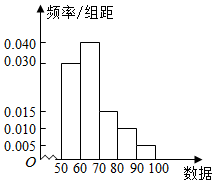• 6．已知一組數據的頻率分布直方圖如圖所示．求眾數、中位數、平均數（　　）

  A．63、64、66

  B．65、65、67

  C．65、64、66

  D．64、65、64
  組卷：182引用：7難度：0.7

  解析

• 7．在區間[-3，3]中隨機取一個實數k,則事件“直線y=kx與圓（x-2）²+y²=1相交”發生的概率為（　　）

  A． 3 9

  B． 3 6

  C． 3 3

  D． 3 2
  組卷：50引用：9難度：0.9

  解析

三、解答題：解答應寫出文字說明，證明過程或演算步驟.

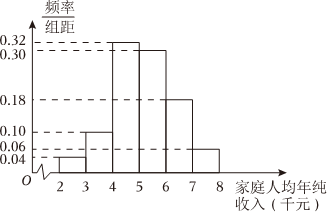• 21．2020年是具有里程碑意義的一年，我們將全面建成小康社會，實現第一個百年奮斗目標；2020年也是脫貧攻堅決戰決勝之年．截至2018年底，中國農村貧困人口從2012年的9899萬人減少至1660萬人，貧困發生率由2012年的10.2%下降至2018年的1.7%；連續7年每年減貧規模都在1000萬人以上；確保到2020年農村貧困人口實現脫貧，是我們黨立下的軍令狀，脫貧攻堅越到最后時刻，越要響鼓重錘．某貧困地區截至2018年底，按照農村家庭人均年純收入8000元的小康標準，該地區僅剩部分家庭尚未實現小康．現從這些尚未實現小康的家庭中隨機抽取50戶，得到這50戶家庭2018年的家庭人均年純收入的頻率分布直方圖．
  （1）假設同組中的每個數據用該組區間的中點值代替，請根據頻率分布直方圖，估計該地區2018年家庭人均年純收入的平均數；
  （2）2019年7月，為估計該地能否在2020年全面實現小康，統計了該地當時最貧困的一個家庭2019年1至6月的人均月純收入如表：
  

  月份/2019（時間代碼x）	1	2	3	4	5	6
  人均月純收入（元）	275	365	415	450	470	485

  由散點圖及相關性分析發現：家庭人均月純收入y與時間代碼x之間具有較強的線性相關關系，試根據表中的數據，求出y關于x的線性回歸方程．
  參考公式和數據：線性回歸方程

  ?

  y

  =

  ?

  b

  x

  +

  ?

  a

  中，

  ?

  b

  =

  n

  ∑

  i

  =

  1

  x

  i

  y

  i

  -

  n

  x

  y

  n

  ∑

  i

  =

  1

  x

  2

  i

  -

  n

  x

  2

  ，

  ?

  a

  =

  y

  -

  ?

  b

  x

  ；

  6

  ∑

  i

  =

  1

  x

  i

  y

  i

  =

  9310

  ．
  組卷：38引用：2難度：0.6

  解析

• 22．（1）已知函數

  f

  （

  x

  ）

  =

  x

  +

  4

  x

  ，

  g

  （

  x

  ）

  =

  2

  x

  +

  a

  ，若對任意的

  x

  1

  ∈

  [

  1

  2

  ，

  1

  ]

  ，

  x

  2

  ∈

  [

  2

  ，

  3

  ]

  ，都有f（x₁）≤g（x₂），求實數a的取值范圍；
  （2）已知函數g（x）=x²-2ax+2a-1，集合A={m|1≤m≤5}，若任意的m∈A，總存在x∈[-2，2]，使得m=g（x）成立，求實數a的取值范圍．
  組卷：48引用：2難度：0.5

  解析