2022-2023學年福建省莆田市八年級(上)期末數學試卷
發布:2024/4/20 14:35:0
一、選擇題:本大題共10小題,每小題4分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.如圖曲線分別是“阿基米德螺線”…“希爾伯特曲線”…“費馬螺線”和“星形線”的一部分.這四種精美的數學曲線中,一定是軸對稱圖形的是( )
A. 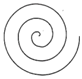
B. 
C. 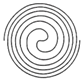
D. 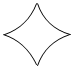 組卷:43引用:2難度:0.8
組卷:43引用:2難度:0.8 -
2.2022年9月9日,中國科學家首次在月球上發現新礦物,并將其命名為“嫦娥石”.在月球樣品顆粒中,分離出一顆粒徑約10微米(即0.00001米)大小的單晶顆粒,并成功解譯其晶體結構,確證為一種新礦物.則數據0.00001用科學記數法表示為( )
A.10×10-6 B.1×10-5 C.1×10-4 D.0.1×10-3 組卷:290引用:9難度:0.8 -
3.若一個多邊形的內角和是540°,則該多邊形的邊數為( )
A.4 B.5 C.6 D.7 組卷:2056引用:73難度:0.9 -
4.(a2)3可以表示成( )
A.3個a2相加 B.5個a相乘 C.2個a3相加 D.3個a2相乘 組卷:209引用:3難度:0.7 -
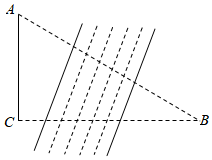 5.如圖,某社會實踐學習小組為測量學校A與河對岸江景房B之間的距離,在學校附近選一點C,利用測量儀器測得∠A=60°,∠C=90°,AC=300米.由此可求得學校與江景房之間的距離AB等于( )
5.如圖,某社會實踐學習小組為測量學校A與河對岸江景房B之間的距離,在學校附近選一點C,利用測量儀器測得∠A=60°,∠C=90°,AC=300米.由此可求得學校與江景房之間的距離AB等于( )A.150米 B.600米 C.800米 D.1200米 組卷:415引用:2難度:0.8 -
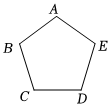 6.如圖,將正五邊形ABCDE置于平面直角坐標系中,若頂點A,B,C,D的坐標分別是(0,a),(-2,-1),(c,m),(d,m),則點E的坐標是( )
6.如圖,將正五邊形ABCDE置于平面直角坐標系中,若頂點A,B,C,D的坐標分別是(0,a),(-2,-1),(c,m),(d,m),則點E的坐標是( )A.(2,-1) B.(2,1) C.(-1,-2) D.(-2,1) 組卷:63引用:2難度:0.5 -
7.從前,古希臘一位莊園主把一塊邊長為a米(a>6)的正方形土地租給租戶張老漢,第二年,他對張老漢說:“我把這塊地的一邊增加6米,相鄰的另一邊減少6米,變成矩形土地繼續租給你,租金不變,你也沒有吃虧,你看如何?”如果這樣,你覺得張老漢的租地面積會( )
A.沒有變化 B.變大了 C.變小了 D.無法確定 組卷:1734引用:23難度:0.7 -
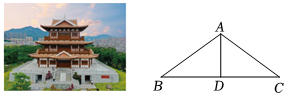 8.“廊橋凌水,樓閣傲天,狀元故里狀元橋,綬溪橋上看綬溪”.莆田綬溪公園開放“狀元橋”和“狀元閣”游覽觀光,其中“狀元閣”的建筑風格堪稱“咫尺之內再造乾坤”.如圖,“狀元閣”的頂端可看作等腰三角形ABC,AB=AC,D是邊BC上的一點.下列條件不能說明AD是△ABC的角平分線的是( )
8.“廊橋凌水,樓閣傲天,狀元故里狀元橋,綬溪橋上看綬溪”.莆田綬溪公園開放“狀元橋”和“狀元閣”游覽觀光,其中“狀元閣”的建筑風格堪稱“咫尺之內再造乾坤”.如圖,“狀元閣”的頂端可看作等腰三角形ABC,AB=AC,D是邊BC上的一點.下列條件不能說明AD是△ABC的角平分線的是( )A.∠ADB=∠ADC B.BD=CD C.BC=2AD D.S△ABD=S△ACD 組卷:412引用:11難度:0.7
三、解答題:本大題共9小題,共86分.解答應寫出必要的文字說明、證明過程、正確作圖或演算步驟.
-
24.某數學興趣小組研究如下等式:38×32=1216,53×57=3021,71×79=5609,84×86=7224.
觀察發現以上等式均是“十位數字相同,個位數字之和是10的兩個兩位數相乘,且積有一定的規律”.
(1)根據上述的運算規律,直接寫出結果:58×52=;752=.
(2)設其中一個數的十位數字為a,個位數字為b(a,b>0),
①請用含a,b的等式表示這個運算規律,并用所學的數學知識證明;
②上述等式中,分別將左邊兩個乘數的十位和個位調換位置,得到新的兩個兩位數相乘(如:38×32調換為83×23).若分別記新的兩個兩位數的乘積為m,①中的運算結果為n,求證:m-n能被99整除.組卷:148引用:4難度:0.6 -
25.如圖1,若P是△ABC內部一點,且∠PAC=∠PCB=∠PBA=α,則稱點P為△ABC的布洛卡點,同時稱α為△ABC的布洛卡角.布洛卡點的發現,引發了研究“三角形幾何”的熱潮.
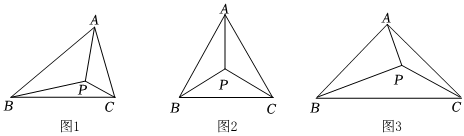
(1)如圖2,P為等邊三角形ABC的布洛卡點,求△ABC的布洛卡角的度數;
(2)如圖3,在△ABC中,AB=AC,P是△ABC內部一點,且∠PAC=∠PCB,∠APC=∠BPC.
①求證:P為△ABC的布洛卡點;
②若∠BAC=∠APB,延長BP交AC于點D,求證:D是AC中點.組卷:189引用:2難度:0.1


