當前位置：試卷中心 > 試卷詳情

2022-2023學年四川省成都市樹德中學高一（下）月考數學試卷（4月份）

發布：2024/7/18 8:0:9

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．半徑為2，圓心角為1弧度的扇形的面積是（　　）
A．1 B．2 C．3 D．4
組卷：264引用：2難度：0.7
解析
2．在△ABC中，“cosA＞cosB”是“A＜B”的（　　）
A．充分必要條件 B．充分不必要條件
C．必要不充分條件 D．既不充分也不必要條件
組卷：67引用：6難度：0.9
解析
3．已知
a
=
（
1
，-
2
）
，
b
=
（
-
2
，
2
）
，則與
a
-
b
同向的單位向量的坐標為（　　）
A．
（
-
3
5
，-
4
5
）
B．
（
3
5
，-
4
5
）
C．
（
3
5
，
4
5
）
D．
（
-
3
5
，
4
5
）
組卷：103引用：2難度：0.8
解析
4．已知向量
a
，
b
滿足
|
a
|
=
1
，
|
b
|
=
2
，
?
a
，
b
?
=
2
π
3
，則
a
?
（
a
+
b
）
=（　　）
A．-2 B．-1 C．0 D．2
組卷：1277引用：20難度：0.7
解析
5．將頂點在原點，始邊為x軸非負半軸的銳角α的終邊繞原點逆時針轉過
π
4
后，交單位圓于點
P
（
-
3
5
，
y
）
，那么cosα的值為（　　）
A．
2
10
B．
2
5
C．
7
2
10
D．
9
2
10
組卷：319引用：5難度：0.7
解析
6．已知α，β∈（0，
π
2
），2tanα=
sin
2
β
sinβ
+
si
n
2
β
，則tan（2α+β+
π
3
）=（　　）
A．
-
3
B．-
3
3
C．
3
3
D．
3
組卷：710引用：9難度：0.8
解析
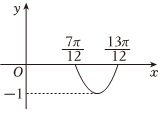7．已知函數f（x）=cos（ωx+φ）（ω＞0，|φ|＜π）的部分圖象如圖所示，且存在0≤x₁＜x₂≤π，滿足
f
（
x
1
）
=
f
（
x
2
）
=
-
4
5
，則cos（x₂-x₁）=（　　）
A．
-
3
5
B．
3
5
C．
4
5
D．
-
4
5
組卷：180引用：3難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，17題10分，剩下每題12分，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．在△ABC中，已知AB=2，AC=1，
AB
?
AC
=
-
1
，
CP
=
λ
CB
（
0
≤
λ
≤
1
）
，Q為線段CA延長線上的一點，且
AQ
=
t
AC
（
t
＜
0
）
．
（1）當t=-1且
λ
=
1
2
，設PQ與AB交于點M，求線段CM的長；
（2）若
PA
?
PQ
+
3
=
AP
?
AB
，求t的最大值．
組卷：51引用：3難度：0.5
解析
22．已知向量
a
=
（
cos
5
x
,
sin
5
x
）
，
b
=
（
2
cos
（
x
-
π
3
）
，
2
sin
（
x
-
π
3
）
）
，令u（x）=
a
?
b
．
（1）求函數u（x）的對稱軸方程；
（2）設
v
（
x
）
=
4
cos
（
2
x
+
π
6
）
，當
x
∈
[
-
π
6
，
π
12
]
時，求函數f（x）=4u（x）-2λv（x）+6λ+5（λ∈R）的最小值g（λ）；
（3）在（2）的條件下，若對任意的實數a,b且a＞b＞0，不等式
t
-
（
1
a
+
1
2
b
）
（
a
+
2
b
）
≤
g
（
λ
）
≤
2
t
+
a
2
+
1
ab
+
1
a
（
a
-
b
）
對任意的λ∈[0，5]恒成立，求實數t的取值范圍．
組卷：922引用：5難度：0.1
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．充分必要條件	B．充分不必要條件
C．必要不充分條件	D．既不充分也不必要條件

2022-2023學年四川省成都市樹德中學高一（下）月考數學試卷（4月份）

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．半徑為2，圓心角為1弧度的扇形的面積是（ ）

2．在△ABC中，“cosA＞cosB”是“A＜B”的（ ）

3．已知a=（1，-2），b=（-2，2），則與a-b同向的單位向量的坐標為（ ）

4．已知向量a，b滿足|a|=1，|b|=2，?a，b?=2π3，則a?（a+b）=（ ）

5．將頂點在原點，始邊為x軸非負半軸的銳角α的終邊繞原點逆時針轉過π4后，交單位圓于點P（-35，y），那么cosα的值為（ ）

6．已知α，β∈（0，π2），2tanα=sin2βsinβ+sin2β，則tan（2α+β+π3）=（ ）

7．已知函數f（x）=cos（ωx+φ）（ω＞0，|φ|＜π）的部分圖象如圖所示，且存在0≤x1＜x2≤π，滿足f（x1）=f（x2）=-45，則cos（x2-x1）=（ ）

四、解答題：本題共6小題，17題10分，剩下每題12分，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．在△ABC中，已知AB=2，AC=1，AB?AC=-1，CP=λCB（0≤λ≤1），Q為線段CA延長線上的一點，且AQ=tAC（t＜0）．（1）當t=-1且λ=12，設PQ與AB交于點M，求線段CM的長；（2）若PA?PQ+3=AP?AB，求t的最大值．

1．半徑為2，圓心角為1弧度的扇形的面積是（　　）

2．在△ABC中，“cosA＞cosB”是“A＜B”的（　　）

3．已知
a
=
（
1
，-
2
）
，
b
=
（
-
2
，
2
）
，則與
a
-
b
同向的單位向量的坐標為（　　）

4．已知向量
a
，
b
滿足
|
a
|
=
1
，
|
b
|
=
2
，
?
a
，
b
?
=
2
π
3
，則
a
?
（
a
+
b
）
=（　　）

5．將頂點在原點，始邊為x軸非負半軸的銳角α的終邊繞原點逆時針轉過
π
4
后，交單位圓于點
P
（
-
3
5
，
y
）
，那么cosα的值為（　　）

6．已知α，β∈（0，
π
2
），2tanα=
sin
2
β
sinβ
+
si
n
2
β
，則tan（2α+β+
π
3
）=（　　）

7．已知函數f（x）=cos（ωx+φ）（ω＞0，|φ|＜π）的部分圖象如圖所示，且存在0≤x₁＜x₂≤π，滿足
f
（
x
1
）
=
f
（
x
2
）
=
-
4
5
，則cos（x₂-x₁）=（　　）

21．在△ABC中，已知AB=2，AC=1，
AB
?
AC
=
-
1
，
CP
=
λ
CB
（
0
≤
λ
≤
1
）
，Q為線段CA延長線上的一點，且
AQ
=
t
AC
（
t
＜
0
）
．
（1）當t=-1且
λ
=
1
2
，設PQ與AB交于點M，求線段CM的長；
（2）若
PA
?
PQ
+
3
=
AP
?
AB
，求t的最大值．