2020-2021學(xué)年江西省景德鎮(zhèn)市九年級(jí)（上）期末數(shù)學(xué)試卷

一、選擇題（本大題共6小題，每小題3分，共18分）

• 1．若正方形的周長(zhǎng)為40，則其對(duì)角線長(zhǎng)為（　　）

  A．100

  B． 40 2

  C．20

  D． 10 2
  組卷：9引用：1難度：0.6

  解析

• 2．已知一元二次方程x²-6x+c=0有一個(gè)根為2，則另一根為（　　）

  A．2

  B．3

  C．4

  D．8
  組卷：1210引用：127難度：0.9

  解析

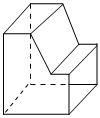• 3．下圖是由一個(gè)長(zhǎng)方體，截去了一部分的得到的幾何體，則其俯視圖是（　　）

  A．

  B．

  C．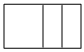

  D．
  組卷：100引用：3難度：0.8

  解析

• 4．關(guān)于x的一元二次方程ax²-bx+1=0中的常數(shù)a和b是-2，0，4中的任意兩個(gè)數(shù)，則該一元二次方程有解的概率為（　　）

  A． 1 2

  B． 1 3

  C． 2 3

  D． 1 4
  組卷：21引用：1難度：0.6

  解析

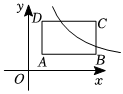• 5．如圖，矩形ABCD在平面直角坐標(biāo)系中，點(diǎn)A（1，1），AB∥x軸，且AB=3，AD=2，若反比例函數(shù)

  y

  =

  k

  x

  與矩形ABCD有交點(diǎn)，則k的取值范圍是（　　）

  A．1＜k＜6

  B．1≤k≤8

  C．1≤k≤10

  D．1≤k≤12
  組卷：442引用：2難度：0.5

  解析

• 6．已知二次函數(shù)y=ax²+bx+c（a＞0）的圖象經(jīng)過(guò)A（0，3），B（4，0）兩點(diǎn)，則關(guān)于該二次函數(shù)圖象的對(duì)稱軸，描述正確的是（　　）

  A．只能是x=3

  B．可能在x=2的右側(cè)

  C．可能是x=2

  D．一定在y軸右側(cè)，且可能在x=4的左側(cè)
  組卷：18引用：1難度：0.6

  解析

二、填空題（本大題共6小題，每小題3分，共18分）

• 7．已知△ABC∽△A₁B₁C₁，△ABC的周長(zhǎng)與△A₁B₁C₁的周長(zhǎng)的比值是

  3

  2

  ，BE、B₁E₁分別是它們對(duì)應(yīng)邊上的中線，且BE=6，則B₁E₁=

   

  ．
  組卷：465引用：2難度：0.7

  解析

五、（本大題共2小題，每小題9分，共18分）

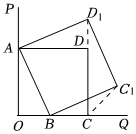• 22．如圖，∠POQ=90°，在∠POQ的內(nèi)部有一個(gè)正方形AOCD，點(diǎn)A，C分別在射線OP，OQ上，點(diǎn)B是OQ上任意一點(diǎn)，在∠POQ的內(nèi)部作正方形ABC₁D₁．
  （1）連接D₁D，求證：∠D₁DA=90°；
  （2）連接CC₁，猜一猜，∠C₁CQ的度數(shù)是多少？證明你的結(jié)論．
  （3）在OQ上再任取一點(diǎn)B₁，以AB₁為邊，在∠POQ的內(nèi)部作正方形AB₁C₂D₂，觀察圖形，可得∠D₂DA=

  ，∠C₂CQ=

  ．
  組卷：107引用：1難度：0.2

  解析

六、（本大題1小題，共12分）

• 23．定義：若二次函數(shù)y=a₁（x-h）²+k的圖象記為C₁，其頂點(diǎn)為A（h,k），二次函數(shù)y=a₂（x-k）²+h的圖象記為C₂，其頂點(diǎn)為B（k,h），我們稱這樣的兩個(gè)二次函數(shù)互為“反頂二次函數(shù)”．
  分類一：若二次函數(shù)C₁：y=a₁（x-h）²+k經(jīng)過(guò)C₂的頂點(diǎn)B，且C₂：y=a₂（x-k）²+h經(jīng)過(guò)C₁的頂點(diǎn)A，我們就稱它們互為“反頂伴侶二次函數(shù)”．
  （1）所有二次函數(shù)都有“反頂伴侶二次函數(shù)”是

  命題．（填“真”或“假”）
  （2）試求出y=x²-4x+5的“反頂伴侶二次函數(shù)”．
  （3）若二次函數(shù)C₁與C₂互為“反頂伴侶二次函數(shù)”，試探究a₁與a₂的關(guān)系，并說(shuō)明理由．
  分類二：若二次函數(shù)C₁：y=a₁（x-h）²+k可以繞點(diǎn)M旋轉(zhuǎn)180°得到二次函數(shù)C₂：y=a₂（x-k）²+h,我們就稱它們互為“反頂旋轉(zhuǎn)二次函數(shù)”．
  ①任意二次函數(shù)都有“反頂旋轉(zhuǎn)二次函數(shù)”是

  命題．（填“真”或“假”）
  ②互為“反頂旋轉(zhuǎn)二次函數(shù)”的對(duì)稱中心點(diǎn)M有什么特點(diǎn)？
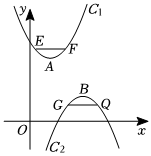
  ③如圖，C₁，C₂互為“反頂旋轉(zhuǎn)二次函數(shù)”，點(diǎn)E，F(xiàn)的對(duì)稱點(diǎn)分別是點(diǎn)Q，G，且EF∥GQ∥x軸，當(dāng)四邊形EFQG為矩形時(shí)，試探究二次函數(shù)C₁，C₂的頂點(diǎn)有什么關(guān)系．并說(shuō)明理由．
  組卷：129引用：1難度：0.1

  解析