2022-2023學年山東省濟南市高二（上）期末數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．等差數列{a_n}中，已知a₂=3，a₅=8，則a₈=（　　）

  A．10

  B．11

  C．12

  D．13
  組卷：182引用：4難度：0.7

  解析

• 2．已知兩個平面的法向量分別為

  m

  =

  （

  0

  ，

  1

  ，

  1

  ）

  ，

  n

  =

  （

  1

  ，-

  1

  ，

  0

  ）

  ，則這兩個平面的夾角為（　　）

  A．30°

  B．60°

  C．60°或120°

  D．120°
  組卷：185引用：5難度：0.7

  解析

• 3．直線l₁：ax+y-1=0與直線l₂：x-ay-1=0的位置關系是（　　）

  A．垂直	B．相交且不垂直
  C．平行	D．平行或重合
  組卷：124引用：5難度：0.7

  解析

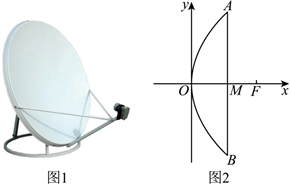• 4．一種衛星接收天線（如圖1），其曲面與軸截面的交線可視為拋物線的一部分（如圖2），已知該衛星接收天線的口徑AB=8米，深度MO=3米，信號處理中心F位于焦點處，以頂點O為坐標原點，建立如圖2所示的平面直角坐標系xOy,則該拋物線的方程為（　　）

  A． y 2 = 4 3 x

  B． y 2 = 16 3 x

  C． y = 4 3 x 2

  D． y = 16 3 x 2
  組卷：77引用：2難度：0.7

  解析

• 5．在等比數列{a_n}中，a₃=

  3

  2

  ，其前三項的和S₃=

  9

  2

  ，則數列{a_n}的公比等于（　　）

  A．- 1 2

  B． 1 2

  C．- 1 2 或1

  D． 1 2 或1
  組卷：146引用：8難度：0.7

  解析

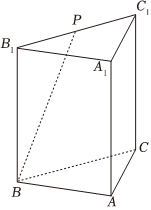• 6．《九章算術》是我國東漢初年編訂的一部數學經典著作，其在卷第五《商功》中記載“斜解立方，得兩塹堵”，塹堵是底面為直角三角形的直三棱柱．如圖，在塹堵ABC-A₁B₁C₁中，AB=AC=AA₁=1，P為B₁C₁的中點，則

  A

  C

  1

  ?

  BP

  =（　　）

  A． 3 2

  B．1

  C． 3 4

  D． 1 2
  組卷：69引用：3難度：0.7

  解析

• 7．若直線y=mx+2與焦點在x軸上的橢圓

  x

  2

  9

  +

  y

  2

  n

  =

  1

  總有公共點，則n的取值范圍是（　　）

  A．（0，4]	B．（4，9）
  C．[4，9）	D．[4，9）∪（9，+∞）
  組卷：301引用：7難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明，證明過程或演算步驟．

• 21．已知橢圓Γ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的長軸長是4，離心率為

  3

  2

  ．
  （1）求Γ的方程；
  （2）若點P是圓O：x²+y²=5上的一動點，過點P作Γ的兩條切線分別交圓O于點A，B．
  ①求證：PA⊥PB；
  ②求△PAB面積的取值范圍．
  組卷：136引用：2難度：0.3

  解析

• 22．對于數列{a_n}，規定數列{Δa_n}為數列{a_n}的一階差分數列，其中Δa_n=a_n+1-a_n，n∈N^*．
  （1）已知數列{a_n}的通項公式為a_n=n³，數列{Δa_n}的前n項和為A_n．
  ①求A_n；
  ②記數列{3n+1}的前n項和為T_n，數列{n²}的前n項和為P_n，且A_n=T_n+λP_n，求實數λ的值．
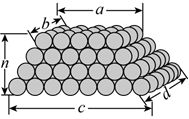
  （2）北宋數學家沈括對于上底有ab個，下底有cd個，共有n層的堆積物（堆積方式如圖），提出可以用公式S=

  n

  6

  [

  （

  2

  b

  +

  d

  ）

  a

  +

  （

  b

  +

  2

  d

  ）

  c

  ]

  +

  n

  6

  （

  c

  -

  a

  ）

  求出物體的總數，這就是所謂的“隙積術”．試證明上述求和公式．
  組卷：84引用：4難度：0.4

  解析