2023-2024學年陜西省寶雞市高新區八年級（上）期中數學試卷

一、選擇題（共8小題，每小題3分，計24分.每小題只有一個選項是符合題意的）

• 1．在數-1、0、

  1

  2

  、

  3

  中，為無理數的是（　　）

  A．-1

  B．0

  C． 1 2

  D． 3
  組卷：395引用：11難度：0.9

  解析

• 2．下列各組數中，能作為直角三角形三邊長的是（　　）

  A．2，3，4

  B． 1 ， 2 ， 3

  C．4，6，8

  D．5，12，15
  組卷：94引用：5難度：0.7

  解析

• 3．點P（2，3）關于x軸的對稱的點的坐標是（　　）

  A．（ 2，-3）

  B．（-2，3）

  C．（2，3）

  D．（-2，-3）
  組卷：1192引用：19難度：0.9

  解析

• 4．下列計算，正確的是（　　）

  A． （ - 3 ） 2 = - 3

  B． 2 + 3 = 5

  C． 4 × 9 = 2 × 3

  D． 12 ÷ 2 = 6
  組卷：125引用：11難度：0.7

  解析

• 5．已知點（-2，y₁），（3，y₂）都在直線y=-x+b上，則y₁與y₂的大小關系是（　　）

  A．y1＜y2

  B．y1=y2

  C．y1＞y2

  D．無法確定
  組卷：606引用：10難度：0.7

  解析

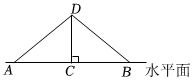• 6．如圖，將長為8cm的橡皮筋放置在水平面上，固定兩端A和B，然后把中點C垂直向上拉升3cm至點D，則橡皮筋被拉長了（　　）

  A．2cm

  B．3cm

  C．4cm

  D．6cm
  組卷：1502引用：13難度：0.8

  解析

• 7．如圖為一次函數y=kx+b的圖象，則一次函數y=bx-k的圖象大致是（　　）

  A．

  B．

  C．

  D．
  組卷：808引用：7難度：0.7

  解析

• 8．成書于大約公元前1世紀的《周髀算經》是中國現存最早的一部數學典籍，里面記載的勾股定理的公式與證明相傳是在西周由商高發現，故又稱之為商高定理．觀察下列勾股數：3，4，5；5，12，13；7，24，25；…，這類勾股數的特點是：勾為奇數，弦與股相差為1；古希臘哲學家柏拉圖（公元前427年—公元前347年）研究了勾為2m（m≥3，m為正整數），弦與股相差為2的一類勾股數，如：6，8，10；8，15，17；…，若此類勾股數的勾為12，則其股為（　　）

  A．14

  B．16

  C．35

  D．37
  組卷：229引用：6難度：0.5

  解析

三、解答題（共13小題，計81分.解答應寫出過程）

• 25．如圖1，同學們想測量旗桿的高度h（米），他們發現系在旗桿頂端的繩子垂到了地面，并多出了一段，但這條繩子的長度未知．小明和小亮同學應用勾股定理分別提出解決這個問題的方案如下：
  
  小明：①測量出繩子垂直落地后還剩余1米，如圖1；
  ②把繩子拉直，繩子末端在地面上離旗桿底部4米，如圖2．
  小亮：先在旗桿底端的繩子上打了一個結，然后舉起繩結拉到如圖3點D處（BD=BC）．
  （1）請你按小明的方案求出旗桿的高度h米；
  （2）已知小亮舉起繩結離旗桿4.5米遠，此時繩結離地面多高？
  組卷：437引用：4難度：0.6

  解析

• 26．如圖，在平面直角坐標系中，一次函數y=-

  1

  2

  x+2的圖象交x軸、y軸分別于點A，B，交直線y=kx于P．
  （1）求點A、B的坐標；
  （2）若OP=PA，求P點坐標及k的值．
  （3）在（2）的條件下，C是直線BP上一動點，CE⊥x軸于E，交直線DP于D，若CD=3ED，直接寫出C點的坐標．
  組卷：1261引用：4難度：0.3

  解析