2022-2023學年江蘇省南京市六校聯考高二（上）期初調研數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．過點A（2，3）且與直線l：2x-4y+7=0平行的直線方程是（　　）

  A．x-2y+4=0

  B．x-2y-4=0

  C．2x-y+1=0

  D．x+2y-8=0
  組卷：715引用：14難度：0.8

  解析

• 2．已知m,n,l是不重合的三條直線，α，β，γ是不重合的三個平面，則（　　）

  A．若m∥n,m?α，則n∥α

  B．若l⊥β，m?α，l⊥m,則α∥β

  C．若m?α，n?α，m∥β，n∥β，則α∥β

  D．若α⊥β，γ⊥β，α∩γ=l,則l⊥β
  組卷：180引用：12難度：0.6

  解析

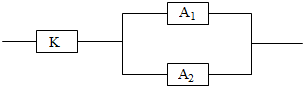• 3．如圖，用K、A₁、A₂三類不同的元件連接成一個系統，當K正常工作且A₁、A₂至少有一個正常工作時，系統正常工作，已知K、A₁、A₂正常工作的概率依次是0.9、0.7、0.7，則系統正常工作概率為（　　）

  A．0.441

  B．0.782

  C．0.819

  D．0.9
  組卷：266引用：8難度：0.7

  解析

• 4．已知圓錐的表面積為6πcm²，且它的側面展開圖是一個半圓，則圓錐的底面半徑為（　　）

  A． 3 2 2 cm

  B． 2 cm

  C． 3 cm

  D．2 3 cm
  組卷：187引用：6難度：0.7

  解析

• 5．點P為x軸上的點，A（-1，2），B（0，3），以A，B，P為頂點的三角形的面積為

  7

  2

  ，則點P的坐標為（　　）

  A．（4，0）或（10，0）	B．（4，0）或（-10，0）
  C．（-4，0）或（10，0）	D．（-4，0）或（11，0）
  組卷：244引用：5難度：0.7

  解析

• 6．對空中飛行的飛機連續射擊兩次，每次發射一枚炮彈，設事件A={兩彈都擊中飛機}，事件B={兩彈都沒擊中飛機}，事件C={恰有一彈擊中飛機}，事件D={至少有一彈擊中飛機}，下列關系不正確的是（　　）

  A．A?D

  B．B∩D=?

  C．A∪C=D

  D．A∪B=B∪D
  組卷：151引用：5難度：0.8

  解析

• 7．若直線l：y=x+b與曲線y=

  4

  -

  x

  2

  有兩個交點，則實數b的取值范圍是（　　）

  A．{b|-2 2 ＜b＜2 2 }

  B．{b|2＜b＜2 2 }

  C．{b|2≤b＜2 2 }

  D．{b|b=±2}
  組卷：606引用：2難度：0.5

  解析

四、解答題：本大題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟．

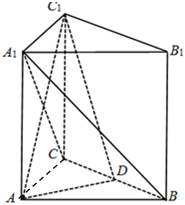• 21．如圖，在直三棱柱ABC-A₁B₁C₁中，AC=BC=CC₁=2，∠ACB=

  π

  2

  ，點D為BC中點．
  （1）求證：平面A₁CB⊥平面AC₁D；
  （2）求點C到平面AC₁D的距離．
  組卷：48引用：2難度：0.4

  解析

• 22．已知⊙C的圓心在直線3x-y-3=0上，點C在y軸右側且到y軸的距離為1，⊙C被直線l：x-y+3=0截得的弦長為2．
  （1）求⊙C的方程；
  （2）設點D在⊙C上運動，且點T滿足

  DT

  =2

  TO

  ，（O為原點）記點T的軌跡為Γ．
  ①求Γ的方程；
  ②過點M（1，0）的直線與Γ交于A，B兩點，問在x軸正半軸上是否存在定點N，使得x軸平分∠ANB？若存在，求出點N的坐標；若不存在，請說明理由．
  組卷：225引用：5難度：0.4

  解析