2022-2023學(xué)年廣東省惠州市惠陽區(qū)良井中學(xué)七年級（上）月考數(shù)學(xué)試卷（9月份）

一、選擇題（共10題，共30分）

• 1．李老師在生物實驗室做實驗時，將水稻種子分組進(jìn)行發(fā)芽實驗，第1組取3粒，第2組取5粒，第3組取7粒…，即每組所取種子數(shù)目比該組前一組增加2粒，按此規(guī)律，那么請你推測第7組應(yīng)取種子粒數(shù)為（　　）

  A．15

  B．13

  C．14

  D．9
  組卷：56引用：3難度：0.7

  解析

• 2．已知整數(shù)a₁、a₂、a₃、a₄、……滿足下列條件：a₁=-1，a₂=-|a₁+1|，a₃=-|a₂+2|，a₄=-|a₃+3|，……，a_n+1=-|a_n+n|（n為正整數(shù)）依此類推，則a₂₀₁₉的值為（　　）

  A．-1007

  B．-1008

  C．-1009

  D．-1010
  組卷：423引用：4難度：0.5

  解析

• 3．若

  1

  x

  =-4，則x的值是（　　）

  A．4

  B． 1 4

  C．- 1 4

  D．-4
  組卷：1137引用：5難度：0.9

  解析

• 4．下列圖形都是由同樣大小的實心圓點按一定規(guī)律組成的，其中第①個圖形一共有5個實心圓點，第②個圖形一共有8個實心圓點，第③個圖形一共有11個實心圓點，…，按此規(guī)律排列下去，第⑥個圖形中實心圓點的個數(shù)為（　　）
  

  A．18

  B．19

  C．20

  D．21
  組卷：1441引用：16難度：0.7

  解析

• 5．已知a是一個正整數(shù)，記G（x）=a-x+|x-a|．若G（1）+G（2）+G（3）+…+G（2019）=90，則a的值為（　　）

  A．8

  B．9

  C．10

  D．11
  組卷：982引用：5難度：0.5

  解析

• 6．一家三口準(zhǔn)備外出旅游，甲乙兩家的旅行社的報價相同，為了競爭，甲旅行社說：“父親買全票，其它人可享受6折優(yōu)惠”．乙旅行社說：“家庭旅行可按團(tuán)體票計價，按原價的

  4

  5

  優(yōu)惠”，由此可以判斷（　　）

  A．甲比乙優(yōu)惠	B．乙比甲優(yōu)惠
  C．甲乙收費相同	D．以上都有可能
  組卷：182引用：4難度：0.9

  解析

• 7．一個機(jī)器人從數(shù)軸的原點出發(fā)，沿數(shù)軸的正方向，以每前進(jìn)3步后退1步的程序運動，設(shè)該機(jī)器人每秒前進(jìn)或后退1步，并且每步的距離為1個單位長度，x_n表示第n秒時該機(jī)器人在數(shù)軸上的位置所對應(yīng)的數(shù)，現(xiàn)給出下列結(jié)論：①x₄=3；②x₈=4；③x₇₉＜x₈₀；④x₁₀₄＜x₁₀₅；⑤x₂₀₁₉＞x₂₀₂₀，其中錯誤的結(jié)論是（　　）

  A．②④⑤

  B．①④

  C．①③

  D．③④
  組卷：13引用：2難度：0.5

  解析

• 8．已知關(guān)于x的多項式-2x³+6x²+9x+1-（3ax²-5x+3）化簡后不含x²項，那么a的值是（　　）

  A．-3

  B．3

  C．-2

  D．2
  組卷：3084引用：11難度：0.8

  解析

三、解答題（共8題，共62分）

• 24．先閱讀下列材料，然后解答問題：
  材料1：從三張不同的卡片中選出兩張排成一列，有6種不同的排法，抽象成數(shù)學(xué)問題就是從3個不同的元素中選取2個元素的排列，排列數(shù)記為A₃²=3×2=6．
  一般地，從n個不同的元素中選取m個元素的排列數(shù)記作A_n^m．A_n^m=n（n-1）（n-2）（n-3）…（n-m+1）（m≤n）
  例：從5個不同的元素中選取3個元素排成一列的排列數(shù)為：A₅³=5×4×3=60．
  材料2：從三張不同的卡片中選取兩張，有3種不同的選法，抽象成數(shù)學(xué)問題就是從3個元素中選取2個元素的組合，組合數(shù)為

  C

  2

  3

  =

  3

  ×

  2

  2

  ×

  1

  =

  3

  ．
  一般地，從n個不同的元素中取出m個元素的排列數(shù)記作A_n^m，
  A_n^m=n（n-1）（n-2）（n-3）…（n-m+1）（m≤n）
  例：從6個不同的元素選3個元素的組合數(shù)為：

  C

  3

  6

  =

  6

  ×

  5

  ×

  4

  3

  ×

  2

  ×

  1

  =

  20

  ．
  問：（1）從某個學(xué)習(xí)小組8人中選取3人參加活動，有

  種不同的選法；
  （2）從7個人中選取4人，排成一列，有

  種不同的排法．
  組卷：3335引用：19難度：0.5

  解析

• 25．問題提出：
  用若干個邊長為1的小等邊三角形拼成n層的大等邊三角形，共需要多少個小等邊三角形？共有線段多少條？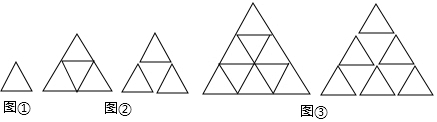
  
  問題探究：
  如圖①，是一個邊長為1的等邊三角形，現(xiàn)在用若干個這樣的等邊三角形再拼成更大的等邊三角形．
  （1）用圖①拼成兩層的大等邊三角形，如圖②，從上往下，第一層有1個，第二層有2個，共用了1+2=3個圖①的等邊三角形，則有長度為1的線段3×（1+2）條；還有邊長為2的等邊三角形1個，則有長度為2的線段3×1條；所以，共有線段3×（1+2+1）=2×（1+2+3）=12條．
  （2）用圖①拼成三層的大等邊三角形，如圖③，從上往下，第一層有1個，第二層有2個，第三層有3個，共用了1+2+3=6個圖①的等邊三角形，則有長度為1的線段3×（1+2+3）條；還有邊長為2的等邊三角形1+2=3個，則有長度為2的線段3×（1+2）條；還有邊長為3的等邊三角形1個，則有長度為3的線段3×1條；所以，共有線段3×（1+2+3+1+2+1）=3×（1+2+3+4）=30條．
  …
  問題解決：
  （3）用圖①拼成四層的大等邊三角形，共需要多少個圖①三角形？共有線段多少條？請在方框中畫出一個示意圖，并寫出探究過程；
  （4）用圖①拼成20層的大等邊三角形，共用了

  個圖①三角形，共有線段

  條．
  組卷：224引用：2難度：0.3

  解析