2023年陜西省漢中市高考數學第二次質檢試卷（文科）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x|x＞1}，B={x|-1＜x＜2}，則A∩B=（　　）

  A．{x|-2＜x＜1}

  B．{x|1＜x＜2}

  C．{x|x＜2}

  D．{x|x＞1}
  組卷：31引用：2難度：0.8

  解析

• 2．復數z=-i（1+2i）在復平面內對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：132引用：2難度：0.9

  解析

• 3．已知向量

  a

  =

  （

  m

  -

  1

  ，

  1

  ）

  ，

  b

  =

  （

  m

  ,-

  2

  ）

  ，且

  a

  ⊥

  b

  ，則m的值為（　　）

  A．-1

  B．1

  C．-1或2

  D．2
  組卷：136引用：3難度：0.8

  解析

• 4．若sin（π-α）=

  1

  3

  ，且

  π

  2

  ≤α≤π，則sin2α的值為（　　）

  A．- 4 2 9

  B．- 2 2 9

  C． 2 2 9

  D． 4 2 9
  組卷：1014引用：18難度：0.9

  解析

• 5．如圖所示，已知兩個線性相關變量x,y的統計數據如下：

  x	6	8	10	12
  y	6	5	3	2

  其線性回歸方程為y=ax+10.3，則a=（　　）

  A．-0.7

  B．0.7

  C．-0.5

  D．-2
  組卷：205引用：4難度：0.8

  解析

• 6．設λ∈R，則“λ=1”是“直線3x+（λ-1）y=1與直線λx+（1-λ）y=2平行”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：261引用：11難度：0.7

  解析

• 7．蚊香具有悠久的歷史，我國蚊香的發明與古人端午節的習俗有關．如圖，為某校數學社團用數學軟件制作的“蚊香”．畫法如下：在水平直線上取長度為1的線段AB，作一個等邊三角形ABC，然后以點B為圓心，AB為半徑逆時針畫圓弧交線段CB的延長線于點D（第一段圓弧），再以點C為圓心，CD為半徑逆時針畫圓弧交線段AC的延長線于點E，再以點A為圓心，AE為半徑逆時針畫圓弧…．以此類推，當得到的“蚊香”恰好有9段圓弧時，“蚊香”的長度為（　　）
  

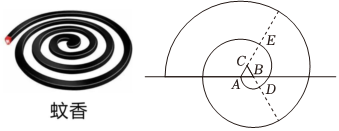
  A．14π

  B．18π

  C．24π

  D．30π
  組卷：306引用：10難度：0.7

  解析

選修4-4：坐標系與參數方程

• 22．在平面直角坐標系xOy中，直線l的參數方程為

  x = 1 + 2 2 t ,

  y = 2 + 2 2 t

  （t為參數），以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，曲線C的極坐標方程為

  ρ

  2

  =

  2

  1

  +

  sin

  2

  θ

  ．
  （1）求直線l的普通方程和曲線C的直角坐標方程；
  （2）設P（1，2），直線l與曲線C交于A，B兩點，求

  1

  |

  PA

  |

  +

  1

  |

  PB

  |

  ．
  組卷：109引用：4難度：0.5

  解析

選修4-5：不等式選講

• 23．設f（x）=|x-1|．
  （1）求f（x）≤2的解集；
  （2）設g（x）=f（x+1）+f（x）的最小值為a,若x+y+z=a（x＞0，y＞0，z＞0），求

  u

  =

  1

  x

  +

  y

  +

  x

  +

  y

  z

  的最小值．
  組卷：22引用：1難度：0.6

  解析