2023-2024學年福建省福州三中高二(上)期中數學試卷
發布:2024/10/21 18:0:2
一、選擇題:本大題共8個小題,每小題5分,共40分.
-
1.已知空間向量
,a,且b,AB=3a+6b,BC=-10a+12b,則一定共線的三點是( )CD=14a-4bA.A、B、C B.B、C、D C.A、B、D D.A、C、D 組卷:70引用:2難度:0.8 -
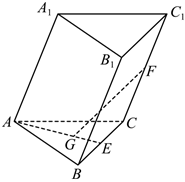 2.如圖,在三棱柱ABC-A1B1C1中,E、F分別是BC、CC1的中點,G為△ABC的重心,則=( )GF
2.如圖,在三棱柱ABC-A1B1C1中,E、F分別是BC、CC1的中點,G為△ABC的重心,則=( )GFA. -13AB+23AC+12AA1B. 13AB+23AC+12AA1C. -23AB+13AC-12AA1D. 13AB-23AC+12AA1組卷:676引用:11難度:0.8 -
3.當圓C:x2+y2+6y-3=0的圓心到直線l:mx+y+m-1=0的距離最大時,m=( )
A. 14B.4 C. -14D.-4 組卷:99引用:3難度:0.8 -
4.已知橢圓C:
的左頂點為A,上頂點為B,右焦點為F,若∠ABF=90°,則橢圓C的離心率為( )x2a2+y2b2=1(a>b>0)A. 5-12B. 3-12C. 1+54D. 3+14組卷:1436引用:16難度:0.7 -
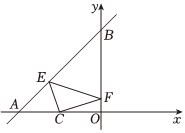 5.如圖,一次函數y=x+3的圖象與x軸,y軸分別交于點A,B,點C(-2,0)是x軸上一點,點E,F分別為直線y=x+3和y軸上的兩個動點,當△CEF周長最小時,點E,F的坐標分別為( )
5.如圖,一次函數y=x+3的圖象與x軸,y軸分別交于點A,B,點C(-2,0)是x軸上一點,點E,F分別為直線y=x+3和y軸上的兩個動點,當△CEF周長最小時,點E,F的坐標分別為( )A. ,F(0,2)E(-136,56)B.E(-2,2),F(0,2) C. ,E(-136,56)F(0,25)D.E(-2,2), F(0,25)組卷:25引用:2難度:0.6 -
6.若直線l:kx-y+3k=0與曲線
有兩個不同的交點,則實數k的取值范圍是( )C:1-x2=y-1A. (12,34]B. [12,34)C. (0,34)D. (0,34]組卷:1639引用:18難度:0.5 -
7.已知過橢圓
左焦點F且與長軸垂直的弦長為C:x2a2+y2b2=1(a>b>0),過點P(2,1)且斜率為-1的直線與C相交于A,B兩點,若P恰好是AB的中點,則橢圓C上一點M到F的距離的最大值為( )62A.6 B. 22+6C. 23+6D. 62+6組卷:215引用:8難度:0.5
四、解答題:本大題共6小題,共70分.
-
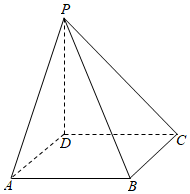 21.如圖,四棱錐P-ABCD的底面為正方形,PD⊥底面ABCD.設平面PAD與平面PBC的交線為l.
21.如圖,四棱錐P-ABCD的底面為正方形,PD⊥底面ABCD.設平面PAD與平面PBC的交線為l.
(1)證明:l⊥平面PDC;
(2)已知PD=AD=1,Q為l上的點,求PB與平面QCD所成角的正弦值的最大值.組卷:8245引用:22難度:0.5 -
22.已知橢圓
過點A(-2,-1),離心率C:x2a2+y2b2=1(a>b>0).e=32
(1)求橢圓C的標準方程;
(2)設過點A的斜率為k直線l交橢圓C于另一點B,若△OAB的面積為2,其中O為坐標原點,求直線l的斜率k的值;
(3)設過點D(-4,0)的直線l′交橢圓C于點M,N,直線MA,NA分別交直線x=-4于點P,Q.求證:線段PQ的中點T為定點.組卷:89引用:2難度:0.5


