2022-2023學年江蘇省南京市雨花臺中學八年級（上）月考數學試卷（10月份）

一、選擇題（本大題共8小題，每小題0分，共16分）

• 1．下列倡導節約的圖案中是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：355引用：27難度：0.9

  解析

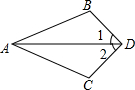• 2．如圖，已知∠1=∠2，則不一定能使△ABD≌△ACD的條件是（　　）

  A．BD=CD

  B．AB=AC

  C．∠B=∠C

  D．∠BAD=∠CAD
  組卷：2735引用：61難度：0.9

  解析

• 3．滿足下列條件的△ABC不是直角三角形的是（　　）

  A．∠A：∠B：∠C=2：3：4	B．∠A：∠B：∠C=1：2：3
  C．∠A-∠B=∠C	D．BC=3，AC=4，AB=5
  組卷：199引用：4難度：0.7

  解析

• 4．在聯歡會上，有A、B、C三名選手站在一個三角形的三個頂點的位置上，他們在玩搶凳子游戲，要求在他們中間放一個木凳，誰先搶到凳子誰獲勝，為使游戲公平，則凳子應放的最適當的位置是在△ABC的（　　）

  A．三邊中線的交點	B．三邊垂直平分線的交點
  C．三條角平分線的交點	D．三邊上高的交點
  組卷：3572引用：96難度：0.7

  解析

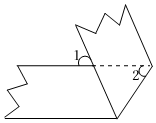• 5．如圖，將一條兩邊沿互相平行的紙帶折疊，若∠1比∠2大12°，則∠1的度數為（　　）

  A．66°

  B．68°

  C．54°

  D．56°
  組卷：928引用：5難度：0.5

  解析

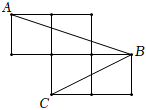• 6．如圖，每個小正方形的邊長為1，若A、B、C是小正方形的頂點，則∠ABC度數為（　　）

  A．60°

  B．45°

  C．30°

  D．20°
  組卷：478引用：3難度：0.7

  解析

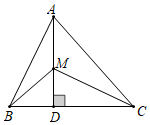• 7．如圖所示，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M為AD上任一點，則MC²-MB²等于（　　）

  A．9

  B．25

  C．36

  D．45
  組卷：1728引用：11難度：0.6

  解析

三、解答題（共68分）

• 22．如圖，在四邊形ABCD中，AD∥BC，AD=2BC，點E是AD的中點，請僅用無刻度的直尺分別按下列要求畫圖．（不寫畫法，保留畫圖痕跡）
  
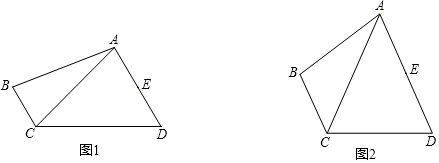
  （1）在圖1中，畫出△ACD的邊AC上的中線DM；
  （2）在圖2中，若AC=AD，畫出△ACD的邊CD上的高AN．
  組卷：1282引用：6難度：0.8

  解析

• 23．背景資料：在已知△ABC所在平面上求一點P，使它到三角形的三個頂點的距離之和最小．這個問題是法國數學家費馬1640年前后向意大利物理學家托里拆利提出的，所求的點被人們稱為“費馬點”．如圖1，當△ABC三個內角均小于120°時，費馬點P在△ABC內部，當∠APB=∠APC=∠CPB=120°時，則PA+PB+PC取得最小值．
  
  （1）如圖2，等邊△ABC內有一點P，若點P到頂點A、B、C的距離分別為3，4，5，求∠APB的度數，為了解決本題，我們可以將△APB繞頂點A旋轉到△ACP'處，此時△ACP'≌△ABP這樣就可以利用旋轉變換，將三條線段PA、PB、PC轉化到一個三角形中，從而求出∠APB=

  ；
  知識生成：怎樣找三個內角均小于120°的三角形的費馬點呢？為此我們只要以三角形一邊在外側作等邊三角形并連接等邊三角形的頂點與△ABC的另一頂點，則連線通過三角形內部的費馬點．請同學們探索以下問題．
  （2）如圖3，△ABC三個內角均小于120°，在△ABC外側作等邊三角形△ABB'，連接CB'，求證：CB'過△ABC的費馬點．
  （3）如圖4，在Rt△ABC中，∠C=90°，AC=1，∠ABC=30°，點P為△ABC的費馬點，連接AP、BP、CP，求PA+PB+PC的值．
  組卷：1615引用：4難度：0.1

  解析