2023-2024學(xué)年北京市海淀區(qū)八一學(xué)校高二（上）月考數(shù)學(xué)試卷（10月份）

一、選擇題：本大題共10小題，每題5分，共50分.在每小題列出的四個選項中，選出符合題目要求的一項.

• 1．已知

  z

  =

  3

  +

  4

  i

  i

  ，求|z|=（　　）

  A．5

  B．13

  C．15

  D．25
  組卷：26引用：2難度：0.8

  解析

• 2．已知向量

  a

  =

  （

  2

  ，

  2

  ，

  1

  ）

  ，

  b

  =

  （

  x

  ,

  2

  ，

  x

  -

  1

  ）

  ，若

  a

  ⊥

  b

  ，則x=（　　）

  A．1

  B．-1

  C．0

  D． 1 2
  組卷：151引用：2難度：0.7

  解析

• 3．在△ABC中，內(nèi)角A，B，C的對邊分別為a,b,c,且b=

  2

  ，c=

  3

  ，C=60°，則角B=（　　）

  A．45°

  B．30°

  C．45°或135°

  D．30°或150°
  組卷：588引用：6難度：0.8

  解析

• 4．要得到函數(shù)

  y

  =

  sin

  （

  2

  x

  -

  π

  3

  ）

  的圖象，只需將函數(shù)y=sin2x的圖象（　　）

  A．向左平移 π 6 個單位長度	B．向右平移 π 6 個單位長度
  C．向左平移 π 3 個單位長度	D．向右平移 π 3 個單位長度
  組卷：872引用：16難度：0.9

  解析

• 5．設(shè)a,b是兩條不同的直線，α，β是兩個不同的平面，則下列命題正確的是（　　）

  A．若α∥β，a?α，b?β，則a∥b	B．若α∩β=a,b∥a,則b∥α
  C．若α⊥β，a?α，b?β，則a∥b	D．若a⊥α，b?β，α∥β，則a⊥b
  組卷：65引用：1難度：0.4

  解析

• 6．已知向量

  a

  =（1，x,2），

  b

  =（0，1，2），

  c

  =（1，0，0），若

  a

  ，

  b

  ，

  c

  共面，則x等于（　　）

  A．-1

  B．1

  C．1或-1

  D．1或0
  組卷：556引用：9難度：0.9

  解析

三、解答題：本大題共4小題，共45分.解答應(yīng)寫出文字說明，演算步驟或證明過程.

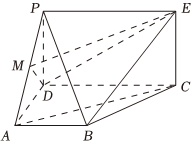• 18．如圖，PDCE為矩形，ABCD為梯形，平面PDCE⊥平面ABCD，∠BAD=∠ADC=90°，

  AB

  =

  AD

  =

  1

  2

  CD

  =

  1

  ，

  PD

  =

  2

  ．
  （1）若M為PA中點，求證：AC∥平面MDE；
  （2）求直線PB與直線CD所成角的大小；
  （3）設(shè)平面PAD∩平面EBC=l,試判斷l(xiāng)與平面ABCD能否垂直？并證明你的結(jié)論．
  
  組卷：141引用：3難度：0.5

  解析

• 19．已知集合S_n={x|x=（x₁，x₂，…，x_n），x_i∈{0，1}，i=1，2，…，n}（n≥2），對于A=（a₁，a₂，…，a_n）∈S_n，B=（b₁，b₂，…，b_n）∈S_n，定義A與B的差為A-B=（|a₁-b₁|，|a₂-b₂|，…，|a_n-b_n|）；A與B之間的距離為d（A，B）=|a₁-b₁|+|a₂-b₂|+…+|a_n-b_n|．
  （Ⅰ）若A-B=（0，1），試寫出所有可能的A，B；
  （Ⅱ）?A，B，C∈S_n，證明：d（A-C，B-C）=d（A，B）；
  （Ⅲ）?A，B，C∈S_n，d（A，B），d（A，C），d（B，C）三個數(shù)中是否一定有偶數(shù)？證明你的結(jié)論．
  組卷：136引用：7難度：0.3

  解析