2022-2023學年浙江省溫州市九年級（上）期末數學試卷

一、選擇題（本題有10小題，每小題3分，共30分。每小題只有一個選項是正確的，不選，多選，錯選均不給分）

• 1．已知⊙O的半徑為5，點P在⊙O內，則OP的長可能是（　　）

  A．7

  B．6

  C．5

  D．4
  組卷：2157引用：35難度：0.9

  解析

• 2．拋物線y=x²-4x+3與y軸的交點坐標為（　　）

  A．（3，0）

  B．（0，3）

  C．（1，0）

  D．（0，1）
  組卷：1248引用：10難度：0.8

  解析

• 3．已知

  a

  b

  =

  3

  4

  ，則

  a

  +

  b

  b

  =（　　）

  A． 1 4

  B． 3 4

  C． 7 4

  D． 4 7
  組卷：340引用：4難度：0.9

  解析

• 4．一個不透明的袋中裝有9個只有顏色不同的球，其中3個紅球，5個白球和1個黃球，從中任意摸出一個球是白球的概率是（　　）

  A． 1 9

  B． 1 3

  C． 5 9

  D． 2 3
  組卷：161引用：2難度：0.7

  解析

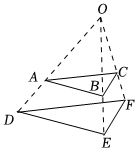• 5．如圖，△ABC與△DEF是位似圖形，點O為位似中心，位似比為2：3，若AB=3，則DE的長為（　　）

  A．4

  B．4.5

  C．5

  D．6
  組卷：740引用：6難度：0.5

  解析

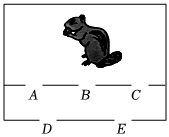• 6．如圖，一只松鼠先經過第一道門（A，B或C），再經過第二道門（D或E）出去，則松鼠走出籠子的路線是“先經過A門，再經過E門”的概率是（　　）

  A． 1 2

  B． 1 3

  C． 1 5

  D． 1 6
  組卷：936引用：10難度：0.7

  解析

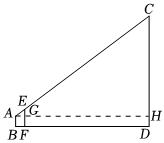• 7．如圖，線段AB，EF，CD分別表示人，竹竿，樓房的高度，且A，E，C在同一直線上．測得人和竹竿的水平距離為1.2m,人和樓房的水平距離為20m,人的高度為1.5m,竹竿的高度為3m,則樓房的高度是（　　）

  A．25m

  B．26.5m

  C．50m

  D．51.5m
  組卷：972引用：2難度：0.5

  解析

• 8．如圖，在△ABC中，∠BAC=90°，AB=6，AC=8．將△ABC繞點A旋轉至△ADE，使AD⊥BC，DE交邊AC于點F，則AF的長是（　　）

  A．4

  B． 24 5

  C．5

  D．6
  組卷：943引用：8難度：0.6

  解析

三、解答題（本題有6小題，共46分，解答需寫出必要的文字說明、演算步驟或證明過程）

• 23．根據素材解決問題．
  

  設計貨船通過圓形拱橋的方案
  素材1	圖1中有一座圓拱石橋，圖2是其圓形橋拱的示意圖，測得水面寬AB=16m,拱頂離水面的距離CD=4m.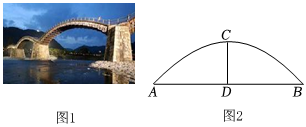
  素材2	如圖3，一艘貨船露出水面部分的橫截面為矩形EFGH，測得EF=3m,EH=10m.因水深足夠，貨船可以根據需要運載貨物．據調查，船身下降的高度y（米）與貨船增加的載重量x（噸）滿足函數關系式 y = 1 100 x ．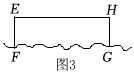
  問題解決
  任務1	確定橋拱半徑	求圓形橋拱的半徑
  任務2	擬定設計方案	根據圖3狀態，貨船能否通過圓形拱橋？若能，最多還能卸載多少噸貨物？若不能，至少要增加多少噸貨物才能通過？
  組卷：2018引用：15難度：0.4

  解析

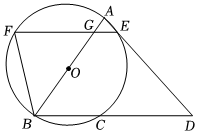• 24．如圖，在⊙O中，直徑AB=10，弦BC=6，點D在BC的延長線上，線段AD
  交⊙O于點E，過點E作EF∥BC分別交⊙O，AB于點F，G，連結BF．
  （1）求證：△ABD∽△FGB．
  （2）當△FGB為等腰三角形時，求CD的長．
  （3）當∠D=45°時，求EG：FG的值．
  組卷：1276引用：3難度：0.1

  解析