當前位置：試卷中心 > 試卷詳情

2023年江西省景德鎮市高考數學第三次質檢試卷（文科）

發布：2024/11/4 6:30:3

一、選擇題：本大題共12小題，每小題5分，共60分，在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知集合A={y|y=sinx}，B=
{
y
|
y
=
-
x
2
+
4
x
-
3
}
，則A∩B=（　　）
A．（1，+∞） B．? C．[0，1] D．（1，3]
組卷：55引用：2難度：0.8
解析
2．若向量
a
=（2，-1）與向量
b
=（1，3）的夾角為θ，則cosθ=（　　）
A．
2
10
B．
-
2
10
C．
2
2
D．
-
2
2
組卷：83引用：2難度：0.8
解析
3．滿足函數f（x）=ln（mx+3）在（-∞，1]上單調遞減的充分必要條件是（　　）
A．-4＜m＜-2 B．-3＜m＜0 C．-4＜m＜0 D．-3＜m＜-1
組卷：57引用：4難度：0.7
解析
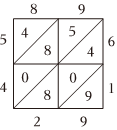4．寫算，是一種格子乘法，也是筆算乘法的一種，用以區別籌算與珠算，它由明代數學家吳敬在其撰寫的《九章算法比類大全》一書中提出，是從天元式的乘法演變而來．例如計算89×61，將被乘數89計入上行，乘數61計入右行，然后以乘數61的每位數字乘被乘數89的每位數字，將結果計入相應的格子中，最后從右下方開始按斜行加起來，滿十向上斜行進一，如圖，即得5429．若從表內的8個數字（含相同的數字，表周邊數據不算在內）中取1個數字，這個數字大于5的概率為（　　）
A．
1
4
B．
3
8
C．
1
2
D．
5
8
組卷：20引用：2難度：0.7
解析
5．一個幾何體的三視圖如圖所示，則該幾何體的體積是（　　）
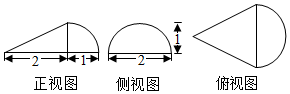
A．
2
π
3
B．3 C．π D．
5
π
3
組卷：31引用：3難度：0.6
解析
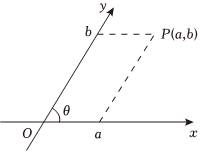6．互相垂直且有公共原點的兩條數軸構成平面直角坐標系，但如果平面坐標系中兩條坐標軸不垂直，則這樣的坐標系稱為“斜坐標系”．如圖，在斜坐標系中，過點P作兩坐標軸的平行線，其在x軸和y軸上的截距a,b分別作為點P的x坐標和y坐標，記P（a,b）．若斜坐標系中，x軸正方向和y軸正方向的夾角為
π
3
，則該坐標系中M（2，2）和N（4，1）兩點間的距離為（　　）
A．2 B．1 C．
5
D．
3
組卷：81引用：2難度：0.6
解析
7．首鋼滑雪大跳臺是冬奧史上第一座與工業舊址結合再利用的競賽場館，它的設計創造性地融入了敦煌壁畫中飛天的元素，建筑外形優美流暢，飄逸靈動，被形象地稱為雪飛天．中國選手谷愛凌和蘇翊鳴分別在此摘得女子自由式滑雪大跳臺和男子單板滑雪大跳臺比賽的金牌．雪飛天的助滑道可以看成一個線段PQ和一段圓弧
?
QM
組成，如圖所示．在適當的坐標系下圓弧
?
QM
所在圓的方程為（x+10）²+（y-3）²=128，若某運動員在起跳點M以傾斜角為45°且與圓C相切的直線方向起跳，起跳后的飛行軌跡是一個對稱軸在y軸上的拋物線的一部分，如圖所示，則該拋物線的軌跡方程為（　　）
A．x²=-4（y+4） B．
y
=
-
1
2
x
2
-
3
C．x²=-32（y-1） D．
y
2
=
-
1
4
（
x
+
4
）
組卷：58引用：8難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

（二）選考題：共10分．請考生在第22、23題中任選一題做答．如果多做，則按所做的第一題記分.

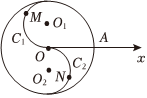22．如圖，在極坐標系Ox中，圓O的半徑為2，半徑均為1的兩個半圓弧C₁，C₂所在圓的圓心分別為
O
1
（
1
，
π
2
）
，
O
2
（
1
，
3
π
2
）
，M是半圓弧C₁上的一個動點，N是半圓弧C₂上的一個動點．
（1）若∠O₂ON=
π
3
，求點N的極坐標；
（2）若點K是射線θ=
π
3
，（ρ≥0）與圓O的交點，求△MOK面積的取值范圍．
組卷：102引用：8難度：0.5
解析