當前位置：試卷中心 > 試卷詳情

2022-2023學年河南省鄭州第二高級中學高二（上）月考數學試卷（10月份）

發布：2024/4/20 14:35:0

2．下列說法中正確的是（　　）

A．

=k表示過點P₁（x₁，y₁），且斜率為k的直線方程

B．直線y=kx+b與y軸交于一點B（0，b），其中截距b=|OB|

C．在x軸和y軸上的截距分別為a與b的直線方程是

D．方程（x₂-x₁）（y-y₁）=（y₂-y₁）（x-x₁）表示過點P₁（x₁，y₁），P₂（x₂，y₂）的直線

組卷：803引用：5難度：0.9

3．已知空間向量
a
，
b
，
c
是一組單位正交向量，
m
=
-
a
+
6
b
-
5
c
，
n
=
3
a
+
8
b
，則
m
?
n
=（　　）
A．15 B．21 C．45 D．36
組卷：40引用：3難度：0.8
解析
4．如果A?B＞0且B?C＜0，那么直線Ax+By+C=0不經過（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：288引用：3難度：0.5
解析
5．已知空間四邊形OABC，M，N分別是對邊OA，BC的中點，點G在線段MN上，且，設
OG
=x
OA
+y
OB
+z
OC
，則x,y,z的值分別是（　　）
A．x=
1
3
，y=
1
3
，z=
1
3
B．x=
1
3
，y=
1
3
，z=
1
6
C．x=
1
3
，y=
1
6
，z=
1
3
D．x=
1
6
，y=
1
3
，z=
1
3
組卷：135引用：2難度：0.9
解析
6．直線xsinα+y+2=0的傾斜角的取值范圍是（　　）
A．[0，π） B．[0，
π
4
]∪[
3
π
4
，π）
C．[0，
π
4
] D．[0，
π
4
]∪（
π
2
，π）
組卷：4008引用：75難度：0.9
解析
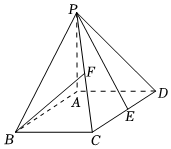7．如圖，在四棱錐P-ABCD中，PA⊥底面ABCD，底面ABCD為正方形，PA=BC，E為CD的中點，F為PC的中點，則異面直線BF與PE所成角的正弦值為（　　）
A．
78
9
B．
8
9
C．
5
3
9
D．
4
5
9
組卷：258引用：16難度：0.7
解析

21．在平面直角坐標系中，直線l過點P（1，2）．
（1）若直線l在兩坐標軸上的截距相等，求直線l的方程；
（2）若直線l分別與x軸正半軸、y軸正半軸交于A、B點，當△AOB面積最小時，求直線l的方程．
組卷：101引用：5難度：0.7
解析
22．如圖，在梯形ABCD中，AB∥CD，∠DAB=90°，
AD
=
DC
=
1
2
AB
=
1
，四邊形ACFE為正方形，平面ACFE⊥平面ABCD．
（1）求證：平面BCF⊥平面ACFE；
（2）點M在線段EF上運動，是否存在點M使平面MAB與平面ACFE所成二面角的平面角的余弦值為
2
3
，若存在，求線段FM的長，若不存在，說明理由．
組卷：74引用：5難度：0.5
解析

A．x= 1 3 ，y= 1 3 ，z= 1 3	B．x= 1 3 ，y= 1 3 ，z= 1 6
C．x= 1 3 ，y= 1 6 ，z= 1 3	D．x= 1 6 ，y= 1 3 ，z= 1 3

A．[0，π）	B．[0， π 4 ]∪[ 3 π 4 ，π）
C．[0， π 4 ]	D．[0， π 4 ]∪（ π 2 ，π）