2022年山東省青島實驗中學中考數學二模試卷

一、選擇題（本題共8小題，每小題3分，共24分）在每小題的四個選項中，只有一項符合要求．

• 1．-

  5

  4

  的相反數是（　　）

  A．- 4 5

  B． 5 4

  C．- 5 4

  D． 4 5
  組卷：1828引用：24難度：0.9

  解析

• 2．下列圖形中，既是軸對稱圖形，又是中心對稱圖形的是（　　）

  A．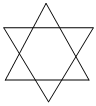

  B．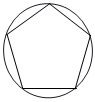

  C．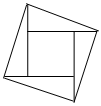

  D．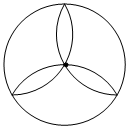
  組卷：36引用：1難度：0.9

  解析

• 3．已知空氣的單位體積質量為1.24×10^-3克/厘米³，1.24×10^-3用小數表示為（　　）

  A．0.000124

  B．0.0124

  C．-0.00124

  D．0.00124
  組卷：1397引用：100難度：0.9

  解析

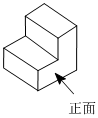• 4．如圖是某個模型，則它的俯視圖是（　　）

  A．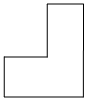

  B．

  C．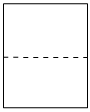

  D．
  組卷：49引用：1難度：0.7

  解析

• 5．有一個兩位數和一個一位數，它們的和為39，若將兩位數放在一位數的前面，得到的三位數比將一位數放在兩位數的前面得到的三位數大27，求這兩個數．若設兩位數是x,一位數是y,則可列方程組為（　　）

  A． x + y = 39 xy - yx = 27

  B． x + y = 39 10 x + y + 27 = 100 y + x

  C． x + y = 39 10 x + y - 27 = 10 y + x

  D． x + y = 39 10 x + y - （ 100 y + x ） = 27
  組卷：1535引用：8難度：0.7

  解析

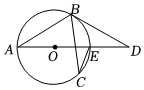• 6．如圖，BD是⊙O的切線，∠BCE=32°，則∠D=（　　）

  A．32°

  B．29°

  C．26°

  D．28°
  組卷：113引用：1難度：0.7

  解析

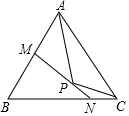• 7．如圖，已知△ABC中，∠B=50°，P為△ABC內一點，過點P的直線MN分別交AB，BC于點M、N．若M在PA的中垂線上，N在PC的中垂線上，則∠APC的度數為（　　）

  A．100°

  B．105°

  C．115°

  D．120°
  組卷：1581引用：8難度：0.6

  解析

• 8．已知在同一平面直角坐標系中二次函數y=mx²+nx和反比例函數y=

  a

  x

  的圖象如圖所示，則一次函數y=

  a

  m

  x-n的圖象可能是（　　）

  A．

  B．

  C．

  D．
  組卷：664引用：5難度：0.6

  解析

三、解答題

• 23．提出問題：把1到2022這2022個數，按順時針方向依次排列在一個圓周上，從1開始按順時針方向，保留1，擦去2，保留3，擦去4……（每隔一數；擦去一數），轉圈擦下去，最后剩下的是哪個數？
  
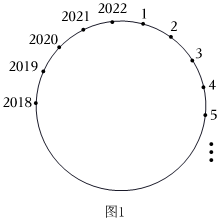
  問題探究：我們先從簡單情形入手，再逐次遞進，最后猜想得出結論．
  探究一：
  如果只有1，2，很明顯，留下1，擦去2，最后剩下1；
  如果只有1，2，3，4，如圖2所示，第一圈留下1，3擦去2，4；第二圈留下1，擦去3，最后剩下1；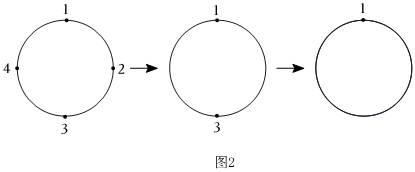
  
  如果只有1，2，3，4，5，6，7，8，如圖3所示，第一圈留下1，3，5，7擦去2，4，6，8；第二圈留下1，5擦去3，7；第三圈留下1，擦去5；最后剩下1；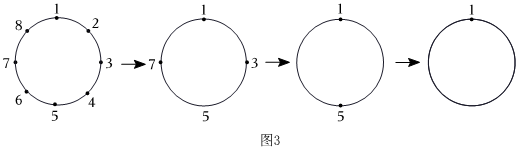
  
  如果只有1，2，3，…，16這16個數，按順時針方向依次排列在一個圓周上，從1開始按順時針方向，保留1，擦去2，保留3，擦去4…（每隔一數，擦去一數），轉圈擦下去，最后剩下的數是

  ；
  探究二：
  如果只有1，2，3，4，5，6，7這7個數，由探究一可知只有4個數時，最后剩下的是1，即4個數中的“第一個數”，因此只要剩下4個數，即可知最后剩下的是哪個數．也就是先擦掉7-4=3個數，擦掉的第3個數是6，它的下一個數是7，也就是剩下的4個數中的第一個是7，所以最后剩下的數就是7；
  如果只有1，2，3，…，12這12個數，由探究一可知只有8個數時，最后剩下的是1，即8個數中的“第一個數”，因此只要剩下8個數，即可知最后剩下的是哪個數．也就是先擦掉12-8=4個數，擦掉的第4個數是8，它的下一個數是9，也就是剩下的8個數中的第一個是9，所以最數學試題第7頁共8頁后剩下的數就是9；
  仿照上面的探究方法，回答下列問題：
  如果只有1，2，3，…，26這26個數，按順時針方向依次排列在一個圓周上，從1開始按順時針方向，保留1，擦去2，保留3，擦去4……（每隔一數，擦去一數），轉圈擦下去，最后剩下的數是

  ；
  問題解決：
  把1到2022這2022個數，按順時針方向依次排列在一個圓周上，從1開始按順時針方向，保留1，擦去2，保留3，擦去4……（每隔一數，擦去一數），轉圈擦下去，最后剩下的數是

  ；
  一般規律：
  把1，2，3，…，n這個數，按順時針方向依次排列在一個圓周上，從1開始按順時針方向，保留1，擦去2，保留3，擦去4……（每隔一數，擦去一數），轉圈擦下去，如果2^k＜n＜2^k+1，且n和k都是正整數，則最后剩下的數是

  ；（用n、k的代數式表示）
  拓展延伸：
  如果只有1，2，3，…，n這n個數，且n5000，n是正整數，按順時針方向依次排列在一個圓周上，從1開始按順時針方向，保留1，擦去2，保留3，擦去4…（每隔一數，擦去一數），轉圈擦下去，如果最后剩下的數是2023，則n可以為

  ．
  組卷：317引用：2難度：0.2

  解析

• 24．如圖，四邊形ABCD中，AD∥BC，∠D=90°，AD=8，BC=CD=6，BE⊥AD于點E，線段BE沿BC以每秒1個單位的速度向點C運動，移動的BE為線段NP，點M從點D出發沿DA以每秒2個單位的速度向點A運動．連接AC交NP于點Q，連接MQ，設運動時間為t秒（0≤t≤4）．
  （1）如圖1，連接AN、CP，當t為何值時，四邊形ANCP為平行四邊形；
  （2）設四邊形CQMD面積為S，求S與t之間的函數關系式；
  （3）如圖2，是否存在某一個時刻1，使△CMQ為直角三角形？若存在，求出t的值；若不存在，說明理由；
  （4）是否存在某一個時刻t,使QC平分∠MQN？若存在，求出t的值；若不存在，請說明理由．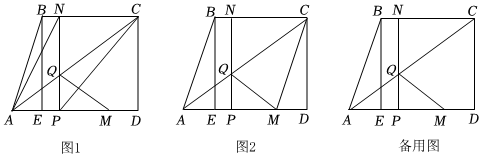
  
  組卷：250引用：1難度：0.3

  解析