2013-2014學(xué)年山東省日照一中高三（下）開學(xué)數(shù)學(xué)試卷（理科）

一、選擇題：本大題共12小題；每小題5分，共60分，在每小題給出的四個選項中，只有一個選項符合題目要求，把正確選項的代號涂在答題卡上．

• 1．設(shè)全集U={1，2，3，4，5，6，7，8，9}，?_U（A∪B）={1，3}，?_UA∩B={2，4}，則集合B=（　　）

  A．{1，2，3，4}

  B．{1，2，3，4，5}

  C．{5，6，7，8，9}

  D．{7，8，9}
  組卷：19引用：4難度：0.9

  解析

• 2．若復(fù)數(shù)z=

  a

  +

  3

  i

  1

  +

  2

  i

  （a∈R）實部與虛部相等，則a的值等于（　　）

  A．-1

  B．3

  C．-9

  D．9
  組卷：32引用：6難度：0.9

  解析

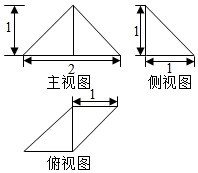• 3．某幾何體的三視圖如圖所示，則該幾何體的體積為（　　）

  A．1

  B． 1 3

  C． 1 2

  D． 3 2
  組卷：2442引用：38難度：0.9

  解析

• 4．設(shè)向量

  a

  =（1，sinθ），

  b

  =（3sinθ，1），且

  a

  ∥

  b

  ，則cos2θ等于（　　）

  A． - 1 3

  B． - 2 3

  C． 2 3

  D． 1 3
  組卷：225引用：14難度：0.9

  解析

• 5．下列推理是歸納推理的是（　　）

  A．A，B為定點，動點P滿足|PA|+|PB|=2a＞|AB|，得P的軌跡為橢圓

  B．由a1=1，an=3n-1，求出S1，S2，S3，猜想出數(shù)列的前n項和Sn的表達式

  C．由圓x2+y2=r2的面積πr2，猜想出橢圓 x 2 a 2 + y 2 b 2 =1的面積S=πab

  D．科學(xué)家利用魚的沉浮原理制造潛艇
  組卷：257引用：30難度：0.9

  解析

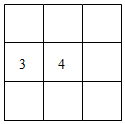• 6．將1，2，3，…，9這9個數(shù)字填在如圖的9個空格中，要求每一行從左到右，每一列從上到下分別依次增大，當(dāng)3，4固定在圖中的位置時，填寫空格的方法數(shù)為（　　）

  A．6種

  B．12種

  C．18種

  D．24種
  組卷：1115引用：18難度：0.7

  解析

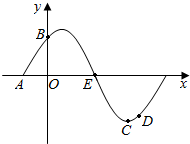• 7．已知A，B，C，D是函數(shù)y=sin（ωx+φ）（ω＞0，0＜φ＜

  π

  2

  ）一個周期內(nèi)的圖象上的四個點，如圖所示，A（-

  π

  6

  ，0），B為y軸上的點，C為圖象上的最低點，E為該圖象的一個對稱中心，B與D關(guān)于點E對稱，

  CD

  在x軸上的投影為

  π

  12

  ，則（　　））

  A．ω=2，φ= π 3

  B．ω=2，φ= π 6

  C．ω= 1 2 ，φ= π 3

  D．ω= 1 2 ，φ= π 6
  組卷：384引用：32難度：0.7

  解析

三、解答題：本大題共6個小題，共74分．解答時要求寫出必要的文字說明、證明過程或推理步驟．

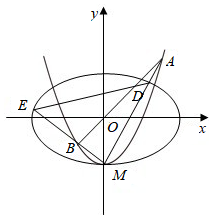• 21．如圖，橢圓

  C

  1

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  2

  2

  ，x軸被曲線

  C

  2

  ：

  y

  =

  x

  2

  -

  b

  截得的線段長等于C₁的短軸長．C₂與y軸的交點為M，過坐標(biāo)原點O的直線l與C₂相交于點A、B，直線MA，MB分別與C₁相交于點D、E．
  （1）求C₁、C₂的方程；
  （2）求證：MA⊥MB．
  （3）記△MAB，△MDE的面積分別為S₁、S₂，若

  S

  1

  S

  2

  =

  λ

  ，求λ的取值范圍．
  組卷：72引用：11難度：0.5

  解析

• 22．已知函數(shù)f（x）=ln

  ex

  2

  -f′（1）?x,g（x）=

  3

  x

  2

  -

  2

  a

  x

  -f（x）（其中a∈R）．
  （1）求f（x）的單調(diào)區(qū)間；
  （2）若函數(shù)g（x）在區(qū)間[2，+∞）上為增函數(shù)，求a的取值范圍；
  （3）設(shè)函數(shù)h（x）=x²-mx+4，當(dāng)a=1時，若存在x₁∈（0，1]，對任意的x₂∈[1，2]，總有g(shù)（x₁）≥h（x₂）成立，求實數(shù)m的取值范圍．
  組卷：90引用：5難度：0.1

  解析