2010-2011學年江蘇省南通市啟東中學高三（上）數學寒假作業試卷（6）

一、填空題：本大題共14小題，每小題5分，共計70分．

• 1．函數f（x）=2sin（3πx-1）（x∈R）的最小正周期為

  ．
  組卷：21引用：6難度：0.9

  解析

• 2．若（1+ai）²=-1+bi（a,b∈R，i是虛數單位），則|a+bi|=

  ．
  組卷：13引用：7難度：0.9

  解析

• 3．某地區在連續7天中，新增某種流感的數據分別為4，2，1，0，0，0，0，則這組數據的方差s²=

  ．
  組卷：20引用：9難度：0.9

  解析

• 4．已知兩個單位向量

  e

  1

  ，

  e

  2

  的夾角為120°，若向量

  a

  =

  e

  1

  +2

  e

  2

  ，b=4e₁，則

  a

  ?

  b

  =

  ．
  組卷：43引用：8難度：0.9

  解析

• 5．已知集合

  A

  =

  {

  x

  |

  x

  =

  nπ

  2

  ，

  n

  =

  0

  ，

  1

  ，

  2

  ，

  3

  ，

  4

  ，

  5

  ，

  6

  }

  ，若從A中任取一個元素x,則恰有cosx=0的概率為

  ．
  組卷：15引用：3難度：0.9

  解析

• 6．在平面直角坐標系xOy中，已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  =

  1

  （a＞0）的一條漸近線與直線l：2x-y+1=0垂直，則實數a=

  ．
  組卷：105引用：13難度：0.7

  解析

• 7．設a,b為不重合的兩條直線，α，β為不重合的兩個平面，給出下列命題：
  （1）若a∥α且b∥α，則a∥b；
  （2）若a⊥α且b⊥α，則a∥b；
  （3）若a∥α且a∥β，則α∥β；
  （4）若a⊥α且a⊥β，則α∥β．
  上面命題中，所有真命題的序號是

  ．
  組卷：70引用：20難度：0.7

  解析

• 8．若等差數列{a_n}的公差為d,前n項的和為S_n，則數列

  {

  S

  n

  n

  }

  為等差數列，公差為

  d

  2

  ．類似地，若各項均為正數的等比數列{b_n}的公比為q,前n項的積為T_n，則數列

  {

  n

  T

  n

  }

  為等比數列，公比為

  ．
  組卷：75引用：10難度：0.7

  解析

三、附加題

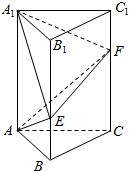• 23．如圖，在直三棱柱ABC-A₁B₁C₁中，∠BAC=90°，AB=AC=a,AA₁=b,點E，F分別在棱BB₁，CC₁上，且

  BE

  =

  1

  3

  B

  B

  1

  ，

  C

  1

  F

  =

  1

  3

  C

  C

  1

  ．設

  λ

  =

  b

  a

  ．當λ=3時，求異面直線AE與A₁F所成角的大小．
  組卷：31引用：5難度：0.5

  解析

• 24．一個袋中裝有黑球，白球和紅球共n（n∈N^*）個，這些球除顏色外完全相同．已知從袋中任意摸出1個球，得到黑球的概率是

  2

  5

  ．現從袋中任意摸出2個球．
  （1）若n=15，且摸出的2個球中至少有1個白球的概率是

  4

  7

  ，設ξ表示摸出的2個球中紅球的個數，求隨機變量ξ的概率分布及數學期望Eξ；
  （2）當n取何值時，摸出的2個球中至少有1個黑球的概率最大，最大概率為多少？
  組卷：384引用：11難度：0.5

  解析