2023-2024學年江蘇省蘇州市吳中區星灣學校八年級（上）期中數學試卷
發布：2024/10/25 1:0:1
一、選擇題（共10小題，每小題2分，共20分）
-
1．全球七大洲的總面積約為149480000km2，這個數據精確到百萬位可表示為（ ）km2，結果用科學記數法表示．
組卷：71引用：4難度：0.7 -
2．下列實數中：0.2020020002…，
，5，0.227，-?8，π2，無理數個數是（ ）39組卷：196引用：3難度：0.7 -
3．如圖，已知AB=CD，從下列條件中補充一個條件后，仍不能判定△ABC≌△CDA的是（ ）組卷：241引用：6難度：0.7 -
4．如圖，在Rt△ABC中，∠B=90°，以點A為圓心，適當長為半徑畫弧，分別交AB、AC于點D，E，再分別以點D、E為圓心，大于為半徑畫弧，兩弧交于點F，作射線AF交邊BC于點G，若BG=1，AC=4，則△ACG的面積是（ ）12DE組卷：422引用：17難度：0.7 -
5．等腰三角形的兩邊a、b滿足
+（b-5）2=0，那么這個三角形的周長是（ ）a-2組卷：461引用：8難度：0.5 -
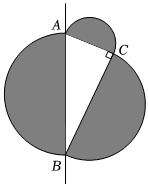6．如圖，在Rt△ABC中，∠C=90°，分別以AB、AC、BC為直徑向外作半圓，它們的面積分別記作S1、S2、S3，若S1=25，S3=16，則S2為（ ）組卷：414引用：2難度：0.5 -
7．如圖，已知△ABC（AC＜BC），用尺規在BC邊上確定一點P，使PA+PC=BC．下面四種作圖中，正確的是（ ）組卷：288引用：4難度：0.7 -
8．下列由三條線段a、b、c構成的三角形：①∠A+∠B=∠C；②a=3k,b=4k,c=5k（k＞0）；③∠A：∠B：∠C=3：4：5；④a=m2+1，b=m2-1，c=2m（m為大于1的整數），其中能構成直角三角形的是（ ）
組卷：1183引用：8難度：0.6 -
9．如圖，△ABC中，AB=BC，∠ABC=84°，∠ABC的平分線與BC的垂直平分線相交于點O，點M、N分別在AB、AC上，點A沿MN折疊后與點O重合，則∠ONC是（ ）
?組卷：564引用：6難度：0.5
三、解答題（共9題，共64分.請把答案填寫在答題卡相應的區域.）
-
26．在等邊△ABC中，點P，Q是BC邊上的兩個動點（不與B，C重合），點P在點Q的左側，且AP=AQ．
（1）若∠BAP=25°，則∠AQB=°；
（2）在圖1中，求證：BP=CQ；
（3）如圖2，點M在邊AC上，CM=CQ，點D為AQ的中點，連接MD并延長交AB于點N，連接PM，PN．猜想△PMN的形狀是 ，并說明理由．
組卷：311引用：2難度：0.5 -
27．定義：三角形中，連接一個頂點和它所對的邊上一點，如果所得線段把三角形的周長分成相等的兩部分，則稱這條線段為三角形的“周長平分線”．
（1）下列與等腰三角形相關的線段中，一定是所在等腰三角形的“周長平分線”的是 （填序號）．
①腰上的高；
②底邊上的中線；
③底角的平分線．
（2）如圖1，在四邊形ABCD中，∠B=∠C=45°，P為BC的中點，∠APD=90°取AD中點Q，連接PQ．
求證：PQ是△APD的“周長平分線”．
（3）在（2）的基礎上，分別取AP，DP的中點M，N，如圖2．請在BC上找點E，F，使EM為△APE的“周長平分線”，FN為△DPF的“周長平分線”．
①用無刻度直尺確定點E，F的位置（保留畫圖痕跡）；
②若AB=2，CD=42，直接寫出EF的長．2
組卷：261引用：1難度：0.1