2022-2023學年湖北省恩施州高中教育聯盟高一（下）期中數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x|x²-1≤0}，B={x|1≤2^x≤4}，則A∩B=（　　）

  A．（0，1]

  B．[0，1]

  C．[-1，0）

  D．[-1，0]
  組卷：56引用：2難度：0.8

  解析

• 2．下列函數中，其定義域和值域分別與y=e^lnx的定義域和值域相同的是（　　）

  A．y=|x|

  B．y= 1 x

  C．y=2x

  D．y=ln|x|
  組卷：130引用：2難度：0.7

  解析

• 3．若命題“?x∈R，x²-4x+a≠0”為假命題，則實數a的取值范圍是（　　）

  A．（-∞，4]

  B．（-∞，4）

  C．（-∞，-4）

  D．[-4，+∞）
  組卷：280引用：10難度：0.7

  解析

• 4．在△ABC中，a=4，b=4

  3

  ，A=30°，則B=（　　）

  A．60°

  B．60°或120°

  C．30°

  D．30°或150°
  組卷：200引用：6難度：0.9

  解析

• 5．已知非零向量

  a

  ，

  b

  ，則“

  |

  a

  -

  b

  |

  =

  |

  b

  |

  ”是“

  a

  -

  2

  b

  =

  0

  ”成立的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：307引用：6難度：0.7

  解析

• 6．已知函數f（x）的圖象的一部分如圖1，則圖2的函數圖象所對應的函數解析式（　　）

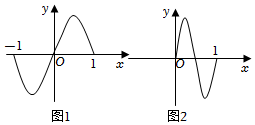
  A．y=f（2x-1）

  B． y = f （ 4 x - 1 2 ）

  C．y=f（1-2x）

  D． y = f （ 1 - 4 x 2 ）
  組卷：52引用：2難度：0.7

  解析

• 7．已知函數f（x）=sinⁿx+cosⁿx（n∈N^*），則下列說法正確的是（　　）
  ①n=1時，f（x）的最大值為

  2

  ；
  ②n=2時，方程f（x）=2sinx+|sinx|在[0，2π]上有且只有三個不等實根；
  ③n=3時，f（x）為奇函數；
  ④n=4時，f（x）的最小正周期為

  π

  2

  ．

  A．①②

  B．①③

  C．②④

  D．①④
  組卷：235引用：2難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．在△ABC中，角A，B，C所對的邊分別為a,b,c,滿足

  cos

  （

  A

  +

  C

  ）

  +

  cos

  （

  A

  -

  C

  ）

  -

  1

  cos

  （

  A

  -

  B

  ）

  +

  cos

  C

  =

  c

  b

  ．
  （1）求B；
  （2）若c=2，點D在邊AC上，且AD=2DC，

  BD

  =

  2

  13

  3

  ，求b.
  組卷：183引用：4難度：0.6

  解析

• 22．已知函數f（x）=x²-mx（m∈R），g（x）=-lnx.
  （1）當m=1時，解方程f（x）=g（x）；
  （2）若對任意的x₁，x₂∈[-1，1]，都有|f（x₁）-f（x₂）|≤2恒成立，試求m的取值范圍；
  （3）用min{m,n}表示m,n中的最小者，設函數

  h

  （

  x

  ）

  =

  min

  {

  f

  （

  x

  ）

  +

  1

  4

  ，

  g

  （

  x

  ）

  }

  （

  x

  ＞

  0

  ）

  ，討論關于x的方程h（x）=0的實數解的個數．
  組卷：172引用：3難度：0.5

  解析